跳到主要内容

深度学习｜求导公式：梯度逆传播规律

· ·
三只鱼
三只鱼
AI Infra Engineer

引言​

我们知道，神经网络的能够学习处理任务的核心是计算损失的梯度，而误差逆传播算法是求梯度的一种通用且高效的办法。使用误差逆传播算法求解神经网络的梯度，其实就是求网络中使用的各种基本运算的局部导数的过程。这期我们将回顾各类基本运算的求导公式，然后演示如何将这些公式运用在误差逆传播算法求解网络梯度。

依赖模块统一导入

此处我们统一导入本文所需的所有依赖模块，下文中不再重复演示。

import numpy as np
import matplotlib.pyplot as plt

作图准备

此处我们准备一个可以绘制下文所有函数图形的 draw 方法，并准备作图用的数据，方便后续演示。

def draw(X, func, func_derivative, title, x_point=1, color='orange', **kwargs):
    """
    绘制函数、切线、导数函数的图形
    :param X: 输入数据
    :param func: 函数
    :param func_derivative: 函数导数
    :param title: 图形标题
    :param x_point: 切线点的 x 轴坐标
    :param color: 图形颜色
    :param kwargs: 函数的参数
    """

    # 创建子图，figsize 参数指定图形的大小为 12 x 5
    fig, axs = plt.subplots(1, 2, figsize=(12, 4.5))

    # 绘制函数图形
    axs[0].plot(X, func(**kwargs)(X), label=title, color=color)
    axs[0].set_title(title)
    axs[0].set_xlabel('Input')
    axs[0].set_ylabel('Output')

    # 绘制在 x_point 处的切线
    func_x_point = func(**kwargs)(x_point)
    func_prime = func_derivative(**kwargs)(x_point)
    tangent_line_func = func_x_point + func_prime * (x - x_point)
    axs[0].plot(x, tangent_line_func,
                label=f"Tangent to {title} at x={x_point}", linestyle=':', color='red')
    axs[0].scatter([x_point], [func_x_point], color='red')

    # legend 函数用于显示图例
    axs[0].legend()
    # grid 函数用于显示网格
    axs[0].grid(True)

    # 绘制导数函数图形
    axs[1].plot(X, func_derivative(**kwargs)(X), label=f"Derivative of {title}", color=color)
    axs[1].set_title(f"Derivative of {title}")
    axs[1].set_xlabel('Input')
    axs[1].set_ylabel('Output')
    axs[1].legend()
    axs[1].grid(True)

    # tight_layout 函数用于调整子图之间的间距
    plt.tight_layout()
    plt.show()

数据准备

# x 从 -2 到 2，等间隔的 400 个点，用于绘制函数图形
x = np.linspace(-2, 2, 400)

基础函数的求导​

常数函数​

常数函数是指函数的值在定义域内保持为常数 cc，即：

f(x)=c f(x) = c

常数函数的导数为零：

ddx[c]=0 \frac{d}{dx}[c] = 0

使用 Python 实现常数函数及其导数：

def constant_function(c):
    return lambda x: np.full_like(x, c)


def constant_derivative(c):
    return lambda x: np.zeros_like(x)

查看常数函数及其导数的图形：

# 绘制常数 c=1 时，常数函数的图形、常数函数在 x=1.0 处的切线、常数函数的导数图形
draw(x, constant_function, constant_derivative, "Constant Function(c=1)", x_point=1.0, color='blue', c=1)

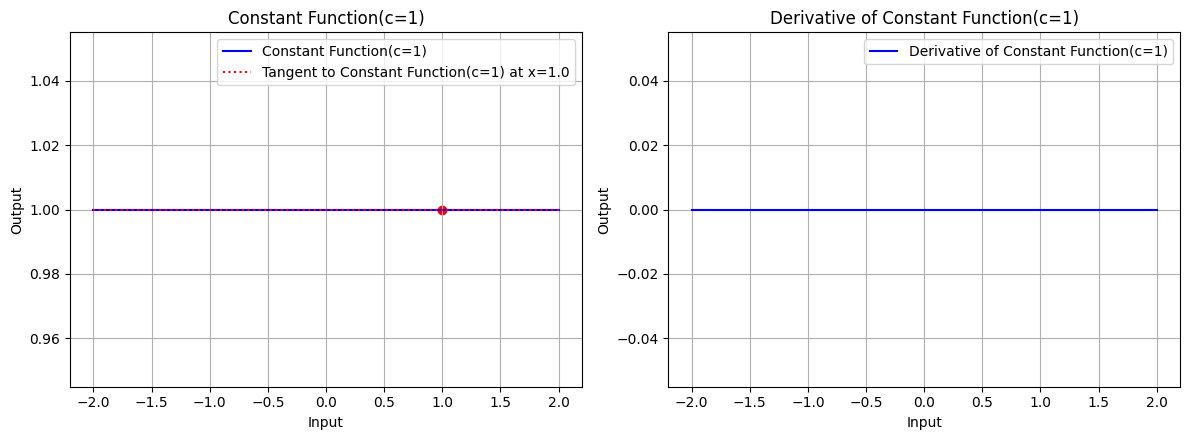
constant-function

图 1：常数 c=1 时，常数函数的图形、常数函数在 x=1.0 处的切线、常数函数的导数图形

常数函数的图形是一条截距为 cc 的水平直线，其导数为零，导数函数的图形是一条全为零的水平直线。

幂函数​

幂函数是指函数的定义域为实数，求关于 xx 的 nn 次幂的函数，其中 nn 是整数，即：

f(x)=xn f(x) = x^n

幂函数 f(x)=xnf(x) = x^n 的导数为：

ddx[xn]=nxn−1 \frac{d}{dx}[x^n] = nx^{n-1}

使用 Python 实现幂函数及其导数：

def power_function(n):
    return lambda x: np.power(x, n)


def power_derivative(n):
    return lambda x: n * np.power(x, n - 1)

查看幂函数及其导数的图形：

# 绘制指数 n=2 时，幂函数的图形、幂函数在 x=1.0 处的切线、幂函数的导数图形
draw(x, power_function, power_derivative, "Power Function(n=2)", x_point=1.0, color='blue', n=2)

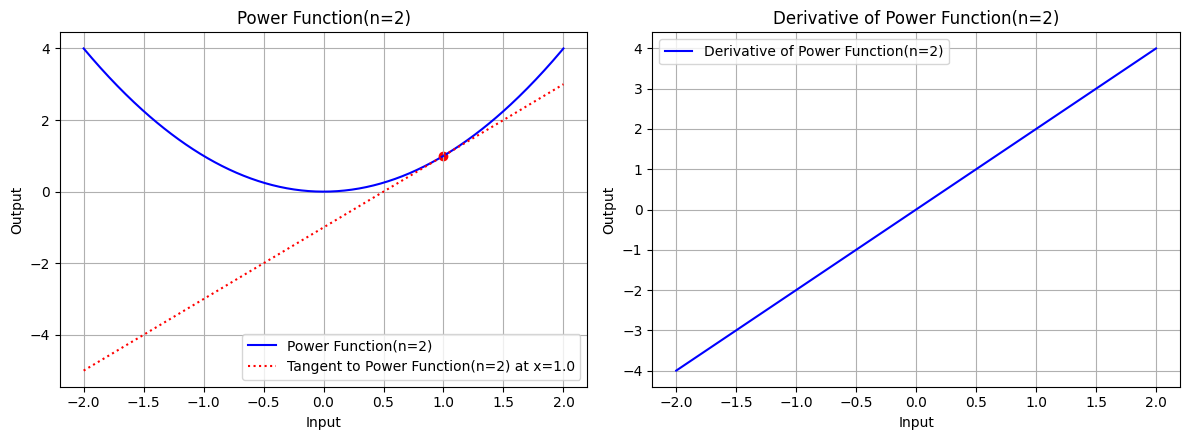
power-function-n-2

图 2.1：指数 n=2 时，幂函数的图形、幂函数在 x=1.0 处的切线、幂函数的导数图形

# 绘制指数 n=3 时，幂函数的图形、幂函数在 x=1.0 处的切线、幂函数的导数图形
draw(x, power_function, power_derivative, "Power Function(n=3)", x_point=1.0, color='blue', n=3)

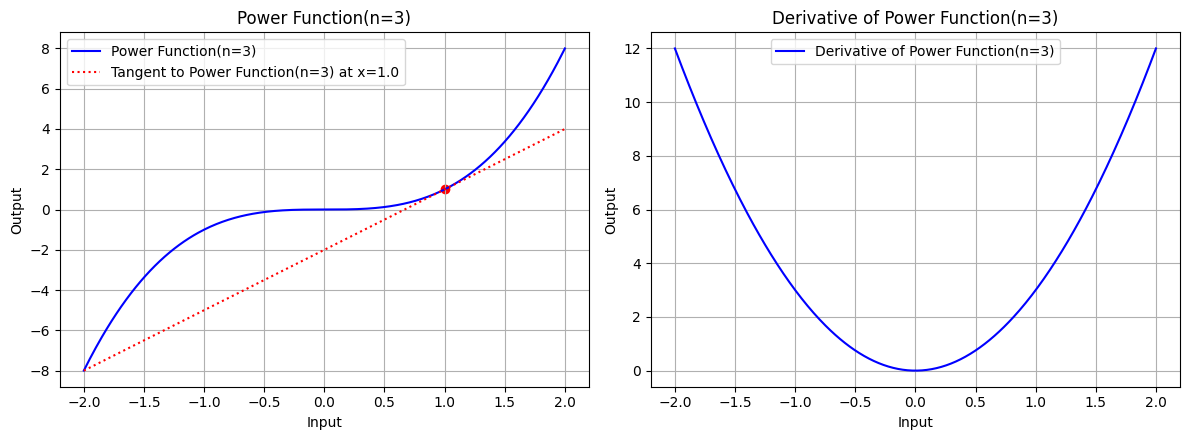
power-function-n-3

图 2.2：指数 n=3 时，幂函数的图形、幂函数在 x=1.0 处的切线、幂函数的导数图形

幂函数的图形是一条经过原点的曲线，其导数为 nxn−1nx^{n-1}，导数函数的图形是一条经过原点的曲线。

指数函数​

指数函数是指函数的定义域为实数，求实数 aa 的 xx 次幂的函数，即：

f(x)=ax f(x) = a^x

指数函数的导数为：

ddx[ax]=axln⁡(a) \frac{d}{dx}[a^x] = a^x \ln(a)

当 a=ea=e 时，这个函数被称为自然指数函数：

f(x)=ex f(x) = e^x

自然指数函数的导数为：

ddx[ex]=ex \frac{d}{dx}[e^x] = e^x

使用 Python 实现指数函数及其导数：

def exp_function(a):
    return lambda x: np.exp(x) if a == np.e else np.power(a, x)


def exp_derivative(a):
    return lambda x: np.exp(x) if a == np.e else np.power(a, x) * np.log(a)

查看指数函数及其导数的图形：

# 绘制底数 a=e 时，指数函数的图形、指数函数在 x=1.0 处的切线、指数函数的导数图形
draw(x, exp_function, exp_derivative, "Exp Function(a=e)", x_point=1.0, color='blue', a=np.e)

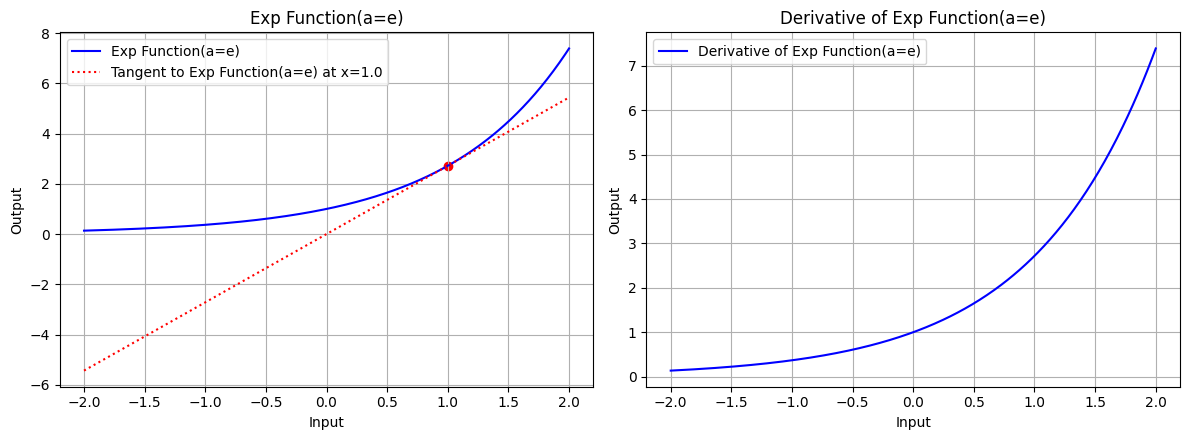
exp-function-a-e

图 3.1：底数 a=e 时，指数函数的图形、指数函数在 x=1.0 处的切线、指数函数的导数图形

draw(x, exp_function, exp_derivative, "Exp Function(a=10)", x_point=1.0, color='blue', a=10)

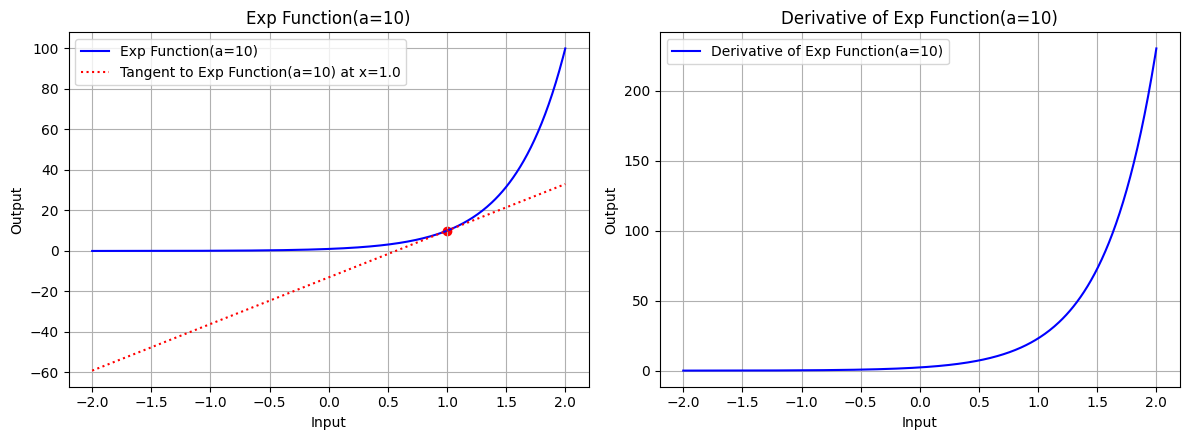
exp-function-a-10

图 3.2：底数 a=10 时，指数函数的图形、指数函数在 x=1.0 处的切线、指数函数的导数图形

对数函数​

对数函数是指函数的定义域为正实数，求底数为 aa 的实数 xx 的对数的函数，即：

f(x)=log⁡a(x) f(x) = \log_a(x)

对数函数的导数为：

ddx[log⁡a(x)]=1xln⁡(a) \frac{d}{dx}[\log_a(x)] = \frac{1}{x \ln(a)}

当底数 a=ea=e 时，我们称这样的对数函数为自然对数函数：

f(x)=ln⁡(x) f(x) = \ln(x)

自然对数函数的导数为：

ddx[ln⁡(x)]=1x \frac{d}{dx}[\ln(x)] = \frac{1}{x}

常用对数 log⁡10(x)\log_{10}(x) 的导数：

ddx[log⁡10(x)]=1xln⁡(10) \frac{d}{dx}[\log_{10}(x)] = \frac{1}{x \ln(10)}

使用 Python 实现对数函数及其导数：

def log_function(base):
    return lambda x: np.log(x) / np.log(base)


def log_derivative(base):
    return lambda x: 1 / (x * np.log(base))

查看对数函数及其导数的图形：

x_log = np.linspace(0.01, 3, 400)
draw(x_log, log_function, log_derivative, "Log Function(base=e)", x_point=1.0, color='blue', base=np.e)

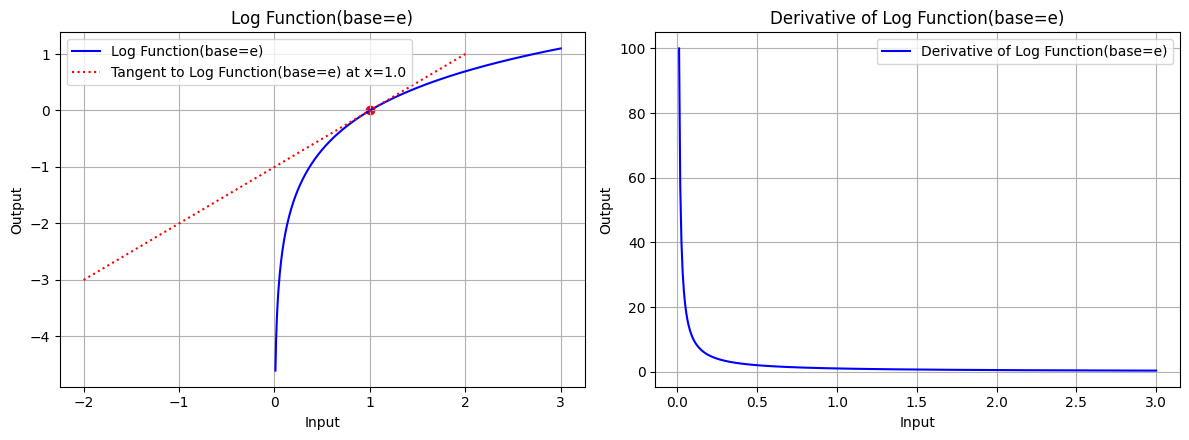
log-function-base-e

图 4.1：底数 base=e 时，对数函数的图形、对数函数在 x=1.0 处的切线、对数函数的导数图形

draw(x_log, log_function, log_derivative, "Log Function(base=10)", x_point=1.0, color='blue', base=10)

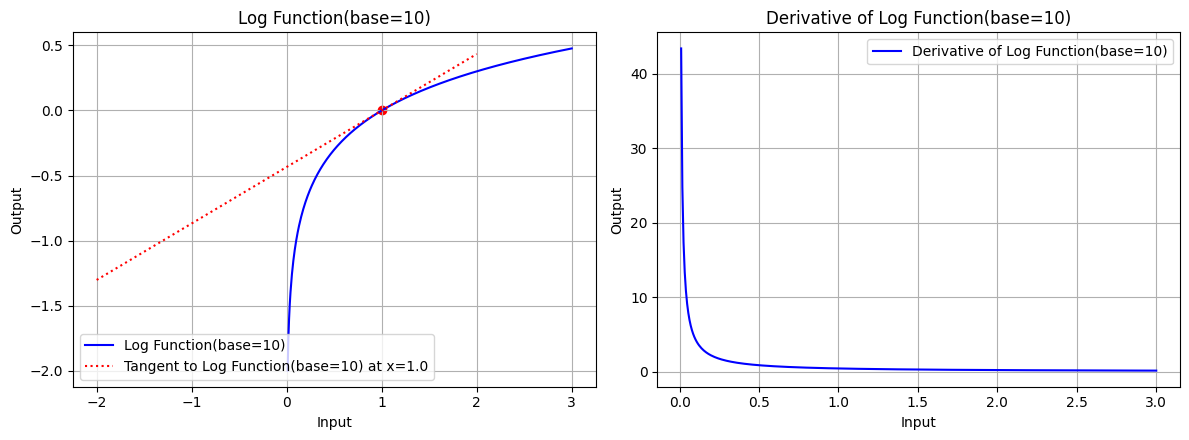
log-function-base-10

图 4.2：底数 base=10 时，对数函数的图形、对数函数在 x=1.0 处的切线、对数函数的导数图形

三角函数​

三角函数是指函数的定义域为实数，求三角形的角度的函数，常见的三角函数包括正弦函数 sin⁡(x)\sin(x)、余弦函数 cos⁡(x)\cos(x) 和正切函数 tan⁡(x)\tan(x)。

正弦函数 sin⁡(x)\sin(x) 的导数：

ddx[sin⁡(x)]=cos⁡(x) \frac{d}{dx}[\sin(x)] = \cos(x)

余弦函数 cos⁡(x)\cos(x) 的导数：

ddx[cos⁡(x)]=−sin⁡(x) \frac{d}{dx}[\cos(x)] = -\sin(x)

正切函数 tan⁡(x)\tan(x) 的导数：

ddx[tan⁡(x)]=sec⁡2(x) \frac{d}{dx}[\tan(x)] = \sec^2(x)

使用 Python 实现三角函数及其导数：

def sin_function():
    return lambda x: np.sin(x)


def sin_derivative():
    return lambda x: np.cos(x)


def cos_function():
    return lambda x: np.cos(x)


def cos_derivative():
    return lambda x: -np.sin(x)


def tan_function():
    return lambda x: np.tan(x)


def tan_derivative():
    return lambda x: 1 / np.cos(x)**2

查看三角函数及其导数的图形：

x_tri = np.linspace(-5, 5, 400)
draw(x_tri, sin_function, sin_derivative, "Sin Function", x_point=1.0, color='blue')

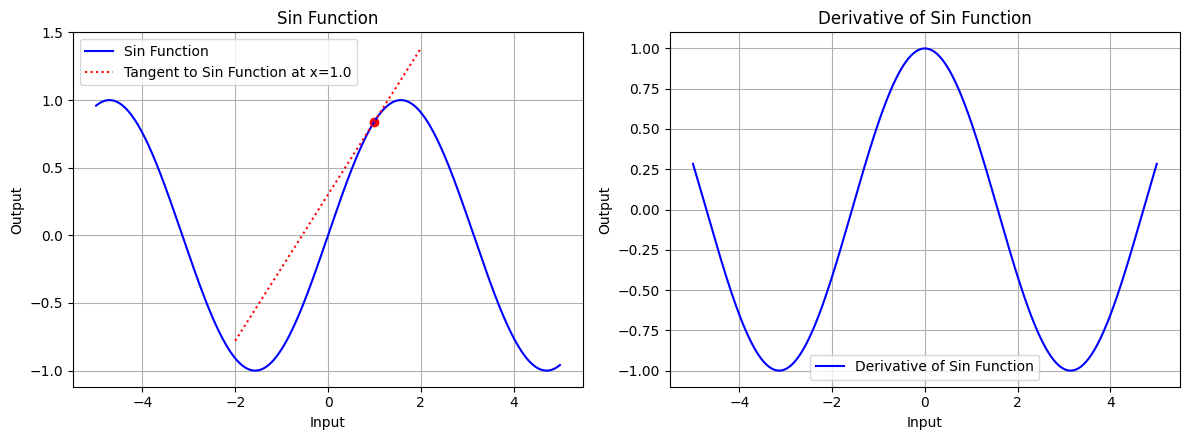
sin-function

图 5.1：正弦函数的图形、正弦函数在 x=1.0 处的切线、正弦函数的导数图形

draw(x_tri, cos_function, cos_derivative, "Cos Function", x_point=1.0, color='blue')

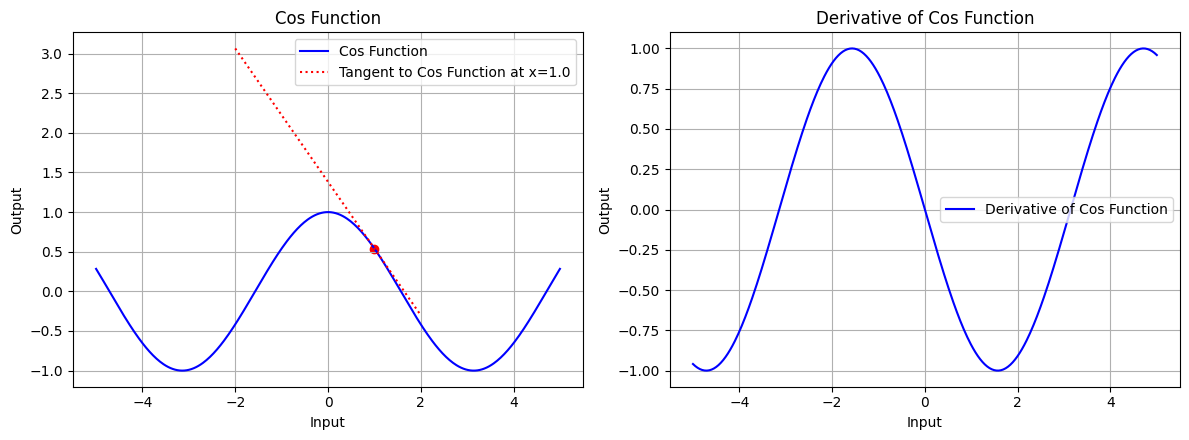
cos-function

图 5.2：余弦函数的图形、余弦函数在 x=1.0 处的切线、余弦函数的导数图形

x_tri = np.linspace(-1.5, 1.5, 100)
draw(x_tri, tan_function, tan_derivative, "Tan Function", x_point=1.0, color='blue')

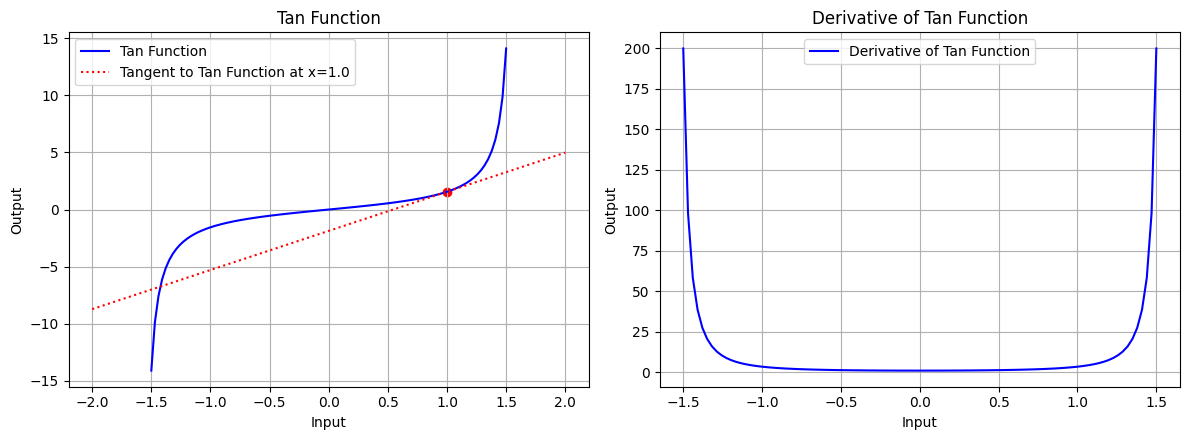
tan-function

图 5.3：正切函数的图形、正切函数在 x=1.0 处的切线、正切函数的导数图形

反三角函数​

反三角函数是指函数的定义域为实数，求三角函数的反函数，常见的反三角函数包括反正弦函数 arcsin⁡(x)\arcsin(x)、反余弦函数 arccos⁡(x)\arccos(x) 和反正切函数 arctan⁡(x)\arctan(x)。

反正弦函数 arcsin⁡(x)\arcsin(x) 的导数：

ddx[arcsin⁡(x)]=11−x2 \frac{d}{dx}[\arcsin(x)] = \frac{1}{\sqrt{1-x^2}}

反余弦函数 arccos⁡(x)\arccos(x) 的导数：

ddx[arccos⁡(x)]=−11−x2 \frac{d}{dx}[\arccos(x)] = -\frac{1}{\sqrt{1-x^2}}

反正切函数 arctan⁡(x)\arctan(x) 的导数：

ddx[arctan⁡(x)]=11+x2 \frac{d}{dx}[\arctan(x)] = \frac{1}{1+x^2}

使用 Python 实现反三角函数及其导数：

def arcsin_function():
    return lambda x: np.arcsin(x)


def arcsin_derivative():
    return lambda x: 1 / np.sqrt(1 - x**2)


def arccos_function():
    return lambda x: np.arccos(x)


def arccos_derivative():
    return lambda x: -1 / np.sqrt(1 - x**2)


def arctan_function():
    return lambda x: np.arctan(x)


def arctan_derivative():
    return lambda x: 1 / (1 + x**2)

查看反三角函数及其导数的图形：

x_atri = np.linspace(-0.999, 0.999, 100)
draw(x_atri, arcsin_function, arcsin_derivative, "ArcSin Function", x_point=0.25, color='blue')

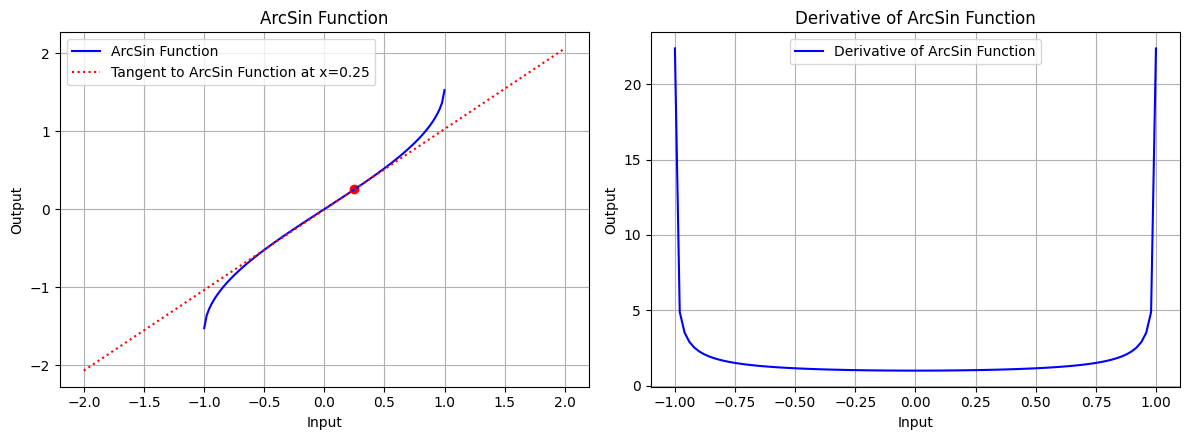
arcsin-function

图 6.1：反正弦函数的图形、反正弦函数在 x=0.25 处的切线、反正弦函数的导数图形

draw(x_atri, arccos_function, arccos_derivative, "ArcCos Function", x_point=0.25, color='blue')

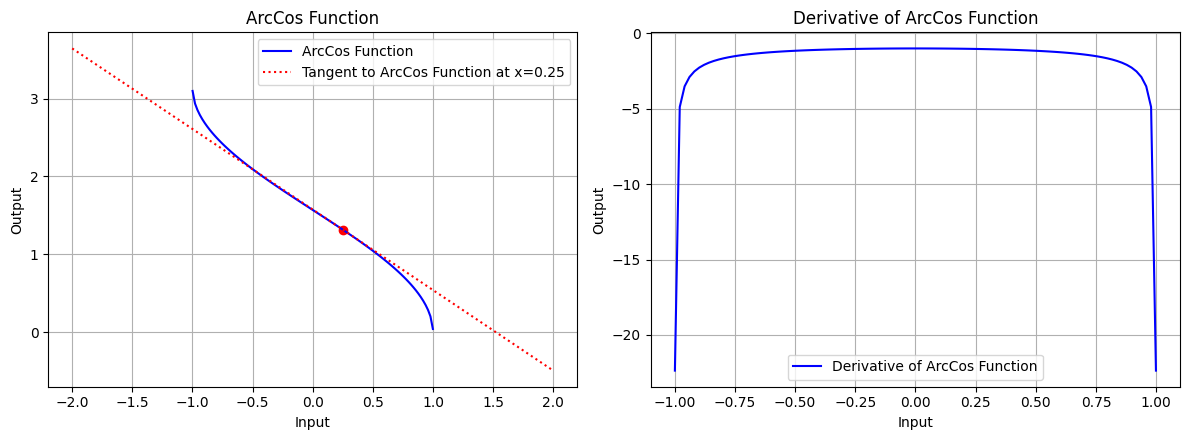
arccos-function

图 6.2：反余弦函数的图形、反余弦函数在 x=0.25 处的切线、反余弦函数的导数图形

x_atri = np.linspace(-5, 5, 100)
draw(x_atri, arctan_function, arctan_derivative, "ArcTan Function", x_point=0.25, color='blue')

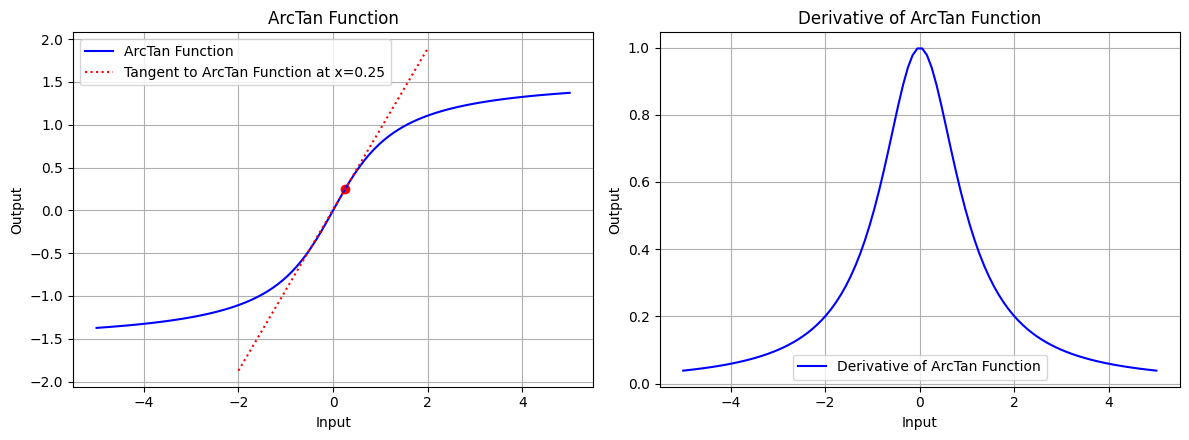
arctan-function

图 6.3：反正切函数的图形、反正切函数在 x=0.25 处的切线、正切弦函数的导数图形

双曲函数​

双曲函数是指函数的定义域为实数，求双曲线的性质的函数，常见的双曲函数包括双曲正弦函数 sinh⁡(x)\sinh(x)、双曲余弦函数 cosh⁡(x)\cosh(x) 和双曲正切函数 tanh⁡(x)\tanh(x)。

双曲函数是在数学中类似于常见三角函数的一类函数，用于描述双曲线的几何性质。双曲函数按照与三角函数相似的方式，但专注于双曲线的性质，描述许多自然现象。双曲函数在物理和工程中有广泛应用，如描述悬链线问题等。它们与指数函数有密切的关系，同时也满足许多类似于三角函数的恒等式。

双曲正弦函数 sinh⁡(x)\sinh(x) 的导数：

ddx[sinh⁡(x)]=cosh⁡(x) \frac{d}{dx}[\sinh(x)] = \cosh(x)

双曲余弦函数 cosh⁡(x)\cosh(x) 的导数：

ddx[cosh⁡(x)]=sinh⁡(x) \frac{d}{dx}[\cosh(x)] = \sinh(x)

双曲正切函数 tanh⁡(x)\tanh(x) 的导数：

ddx[tanh⁡(x)]=sech2(x) \frac{d}{dx}[\tanh(x)] = \text{sech}^2(x)

使用 Python 实现双曲函数及其导数：

def sinh_function():
    return lambda x: np.sinh(x)


def sinh_derivative():
    return lambda x: np.cosh(x)


def cosh_function():
    return lambda x: np.cosh(x)


def cosh_derivative():
    return lambda x: np.sinh(x)


def tanh_function():
    return lambda x: np.tanh(x)


def tanh_derivative():
    return lambda x: 1 / np.cosh(x)**2

查看双曲函数及其导数的图形：

x_trih = np.linspace(-5, 5, 100)
draw(x_atri, sinh_function, sinh_derivative, "SinH Function", x_point=0.25, color='blue')

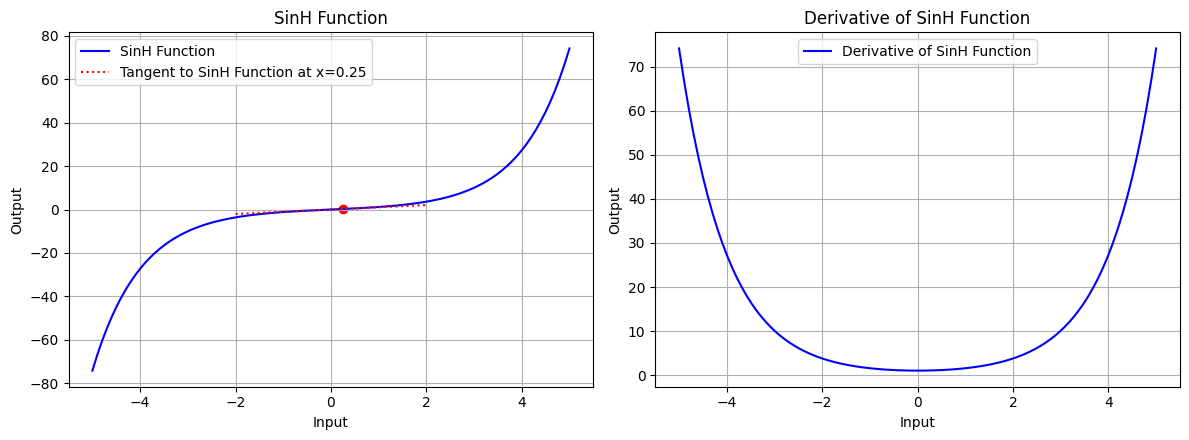
sinh-function

图 7.1：双曲正弦函数的图形、双曲正弦函数在 x=0.25 处的切线、双曲正弦函数的导数图形

draw(x_atri, cosh_function, cosh_derivative, "CosH Function", x_point=0.25, color='blue')

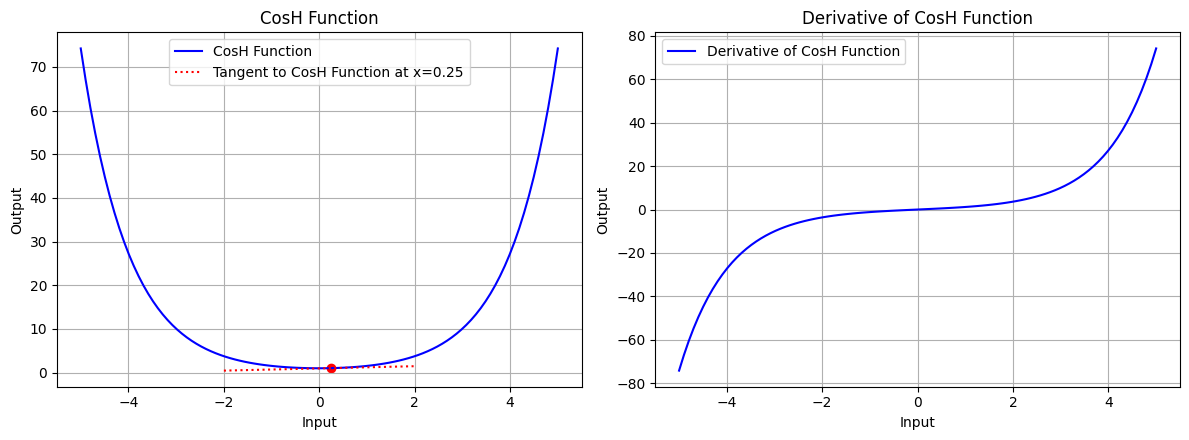
cosh-function

图 7.2：双曲余弦函数的图形、双曲余弦函数在 x=0.25 处的切线、双曲余弦函数的导数图形

draw(x_atri, tanh_function, tanh_derivative, "TanH Function", x_point=0.25, color='blue')

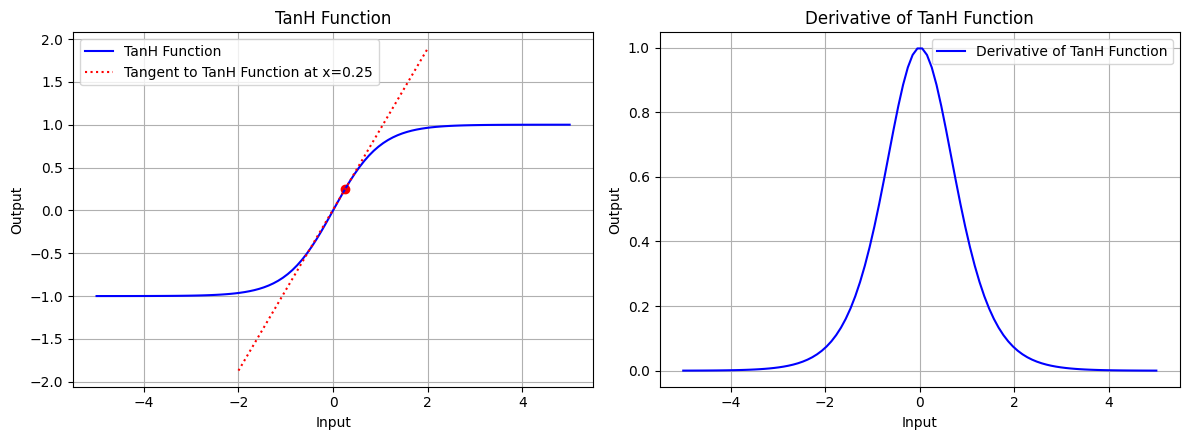
tanh-function

图 7.3：双曲正切函数的图形、双曲正切函数在 x=0.25 处的切线、双曲正切函数的导数图形

复合函数的梯度逆传播​

链式法则​

链式法则描述的是复合函数的导数计算规则，对于复合函数 f(g(x))f(g(x))，其导数为：

ddx[f(g(x))]=f′(g(x))⋅g′(x) \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)

链式法则是微积分中的一个重要概念，用于计算复合函数的导数。在神经网络中，链式法则被广泛应用于计算损失函数对网络参数的梯度。

函数相加​

将两个函数相加得到一个新的函数，即：

f(x)=g(x)+h(x) f(x) = g(x) + h(x)

函数相加所得函数的导数为：

f′(x)=ddx[g(x)+h(x)]=g′(x)+h′(x) f'(x) = \frac{d}{dx}[g(x) + h(x)] = g'(x) + h'(x)

若自变量不唯一，如：

f(x,y)=g(x)+h(y) f(x, y) = g(x) + h(y)

此时，函数相加所得函数关于自变量的偏导数分别为：

∂∂x[f(x,y)]=∂g(x)∂x+∂h(y)∂x=∂g(x)∂x+0=g′(x) \frac{\partial}{\partial x}[f(x, y)] = \frac{\partial g(x)}{\partial x} + \frac{\partial h(y)}{\partial x} = \frac{\partial g(x)}{\partial x} + 0 = g'(x) ∂∂y[f(x,y)]=∂g(x)∂y+∂h(y)∂y=0+∂h(y)∂y=h′(y) \frac{\partial}{\partial y}[f(x, y)] = \frac{\partial g(x)}{\partial y} + \frac{\partial h(y)}{\partial y} = 0 + \frac{\partial h(y)}{\partial y} = h'(y)

f=g+hf = g + h 的计算传播图如下：

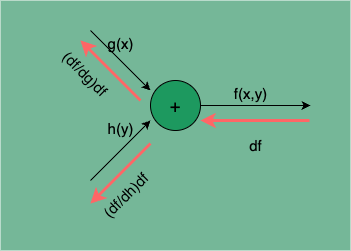
add-bp

图 8：函数相加的计算传播图

g(x)g(x) 处的梯度为：

dfdg×df=dfdxdgdx×df=dgdx+dhdxdgdx×df=dgdx+0dgdx×df=df \frac{df}{dg} \times df = \frac{\frac{df}{dx}}{\frac{dg}{dx}} \times df = \frac{\frac{dg}{dx} + \frac{dh}{dx}}{\frac{dg}{dx}} \times df = \frac{\frac{dg}{dx} + 0}{\frac{dg}{dx}} \times df = df

h(y)h(y) 处的梯度为：

dfdh×df=dfdydhdy×df=dgdy+dhdydhdy×df=0+dhdydhdy×df=df \frac{df}{dh} \times df = \frac{\frac{df}{dy}}{\frac{dh}{dy}} \times df = \frac{\frac{dg}{dy} + \frac{dh}{dy}}{\frac{dh}{dy}} \times df = \frac{0 + \frac{dh}{dy}}{\frac{dh}{dy}} \times df = df

由此可见，函数相加的梯度逆传播是直接将下游梯度 df 传递给上游，不会发生梯度的变化。

函数相乘​

将两个函数相乘得到一个新的函数，即：

f(x)=g(x)⋅h(x) f(x) = g(x) \cdot h(x)

函数相乘所得函数的导数为：

ddx[f(x)g(x)]=f′(x)g(x)+f(x)g′(x) \frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x)

若自变量不唯一，如：

f(x,y)=g(x)⋅h(y) f(x, y) = g(x) \cdot h(y)

此时，函数相乘所得函数关于自变量的偏导数分别为：

∂∂x[f(x,y)]=∂g(x)∂x⋅h(y)+g(x)⋅∂h(y)∂x=∂g(x)∂x⋅h(y)+g(x)⋅0=g′(x)⋅h(y) \frac{\partial}{\partial x}[f(x, y)] = \frac{\partial g(x)}{\partial x} \cdot h(y) + g(x) \cdot \frac{\partial h(y)}{\partial x} = \frac{\partial g(x)}{\partial x} \cdot h(y) + g(x) \cdot 0 = g'(x) \cdot h(y) ∂∂y[f(x,y)]=∂g(x)∂y⋅h(y)+g(x)⋅∂h(y)∂y=0⋅h(y)+g(x)⋅h′(y)=g(x)⋅h′(y) \frac{\partial}{\partial y}[f(x, y)] = \frac{\partial g(x)}{\partial y} \cdot h(y) + g(x) \cdot \frac{\partial h(y)}{\partial y} = 0 \cdot h(y) + g(x) \cdot h'(y) = g(x) \cdot h'(y)

f=g⋅hf = g \cdot h 的计算传播图如下：

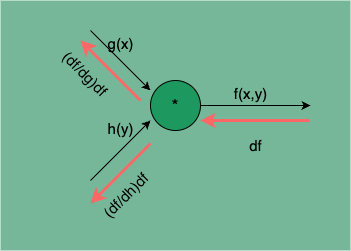
multi-bp

图 9：函数相乘的计算传播图

g(x)g(x) 处的梯度为：

dfdg×df=dfdxdgdx×df=dgdx⋅h(y)+g(x)⋅dhdxdgdx×df=dgdx⋅h(y)+0dgdx×df=h(y)⋅df \begin{split} \frac{df}{dg} \times df = \frac{\frac{df}{dx}}{\frac{dg}{dx}} \times df \\ = \frac{\frac{dg}{dx} \cdot h(y) + g(x) \cdot \frac{dh}{dx}}{\frac{dg}{dx}} \times df \\ = \frac{\frac{dg}{dx} \cdot h(y) + 0}{\frac{dg}{dx}} \times df \\ = h(y) \cdot df \end{split}

h(y)h(y) 处的梯度为：

dfdh×df=dfdydhdy×df=dgdy⋅h(y)+g(x)⋅dhdydhdy×df=0⋅h(y)+g(x)⋅dhdydhdy×df=g(x)⋅df \begin{split} \frac{df}{dh} \times df = \frac{\frac{df}{dy}}{\frac{dh}{dy}} \times df \\ = \frac{\frac{dg}{dy} \cdot h(y) + g(x) \cdot \frac{dh}{dy}}{\frac{dh}{dy}} \times df \\ = \frac{0 \cdot h(y) + g(x) \cdot \frac{dh}{dy}}{\frac{dh}{dy}} \times df \\ = g(x) \cdot df \end{split}

由此可见，函数相乘的梯度逆传播，两个函数 g(x)、h(y) 的梯度分是将下游梯度 df 乘以相乘函数 h(y)、g(x)。

函数相除​

将两个函数相除得到一个新的函数，即：

f(x)=g(x)h(x) f(x) = \frac{g(x)}{h(x)}

函数相除所得函数的导数为：

ddx[g(x)h(x)]=g′(x)h(x)−g(x)h′(x)[h(x)]2 \frac{d}{dx}\left[\frac{g(x)}{h(x)}\right] = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}

若自变量不唯一，如：

f(x,y)=g(x)h(y) f(x, y) = \frac{g(x)}{h(y)}

此时，函数相除所得函数关于自变量的偏导数分别为：

∂∂x[g(x)h(y)]=∂g(x)∂x⋅h(y)−g(x)⋅∂h(y)∂x[h(y)]2=g′(x)⋅h(y)−g(x)⋅0[h(y)]2=g′(x)⋅h(y)[h(y)]2 \begin{split} \frac{\partial}{\partial x}\left[\frac{g(x)}{h(y)}\right] = \frac{\frac{\partial g(x)}{\partial x} \cdot h(y) - g(x) \cdot \frac{\partial h(y)}{\partial x}}{[h(y)]^2} \\ = \frac{g'(x) \cdot h(y) - g(x) \cdot 0}{[h(y)]^2} \\ = \frac{g'(x) \cdot h(y)}{[h(y)]^2} \end{split} ∂∂y[g(x)h(y)]=∂g(x)∂y⋅h(y)−g(x)⋅∂h(y)∂y[h(y)]2=0⋅h(y)−g(x)⋅h′(y)[h(y)]2=−g(x)⋅h′(y)[h(y)]2 \begin{split} \frac{\partial}{\partial y}\left[\frac{g(x)}{h(y)}\right] = \frac{\frac{\partial g(x)}{\partial y} \cdot h(y) - g(x) \cdot \frac{\partial h(y)}{\partial y}}{[h(y)]^2} \\ = \frac{0 \cdot h(y) - g(x) \cdot h'(y)}{[h(y)]^2} \\ = -\frac{g(x) \cdot h'(y)}{[h(y)]^2} \end{split}

f=ghf = \frac{g}{h} 的计算传播图如下：

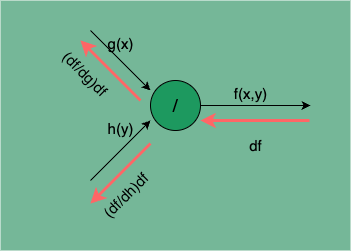
div-bp

图 10：函数相除的计算传播图

g(x)g(x) 处的梯度为：

dfdg×df=dfdxdgdx×df=g′(x)⋅h(y)[h(y)]2g′(x)×df=h(y)[h(y)]2×df=dfh(y) \begin{split} \frac{df}{dg} \times df = \frac{\frac{df}{dx}}{\frac{dg}{dx}} \times df \\ = \frac{\frac{g'(x) \cdot h(y)}{\left[h(y)\right]^2}}{g'(x)} \times df \\ = \frac{h(y)}{[h(y)]^2} \times df \\ = \frac{df}{h(y)} \end{split}

h(y)h(y) 处的梯度为：

dfdh×df=dfdydhdy×df=g(x)⋅h′(y)[h(y)]2h′(y)×df=g(x)[h(y)]2⋅df \begin{split} \frac{df}{dh} \times df = \frac{\frac{df}{dy}}{\frac{dh}{dy}} \times df \\ = \frac{\frac{g(x) \cdot h'(y)}{[h(y)]^2}}{h'(y)} \times df \\ = \frac{g(x)}{[h(y)]^2} \cdot df \end{split}

由此可见，函数相除的梯度逆传播中，被除数 g(x) 的梯度是将下游梯度 df 除以除数 h(y)，除数 h(y) 的梯度是将下游梯度 df 乘以被除数 g(x) 再除以除数的平方 [h(y)]2[h(y)]^2。

结语​

神经网络学习的核心是计算损失函数的梯度，即求损失函数关于网络参数的偏导数。而网络的计算可以理解成一系列基本运算的复合，因此我们可以通过了解这些基本运算的导数求解方式，以及结合链式法则归纳出这些基本运算的复合形式的求导规律，来完成网络的梯度的高效计算。这就是误差逆传播算法的基本原理。

误差逆传播算法是训练人工神经网络最基本的方法，它通过计算每个神经元的梯度，优化网络的权重以使得输出误差最小化。误差逆传播算法是神经网络的学习核心，是它使得人工神经网络成为一种可行的机器学习模型，可以说没有误差逆传播算法就没有今天人工神经网络的流行。

PS：感谢每一位志同道合者的阅读，欢迎关注、点赞、评论！