图论：图的遍历（DFS vs. BFS）

信息

2024年8月26日 · ·

引言

图的遍历是图论中的核心概念，通过不同的遍历方法能够有效地处理多种问题，例如连通性检测、路径查找、图的最小生成树等。本篇我们将重点探讨图的深度优先搜索（DFS）和广度优先搜索（BFS）两种常见的图遍历方法，分析它们的原理、应用场景以及实现方法，并通过实际案例代码分析问题解决方案。

基本概念

图是一种表示对象间关系的数据结构，由顶点和边组成。按照边的方向，图可以分为有向图和无向图。图的遍历主要有两种方式：

• 深度优先搜索（DFS）：优先深入图的分支，直到无法继续时回溯。
• 广度优先搜索（BFS）：优先探索与当前节点相邻的节点，然后逐层向外扩展。

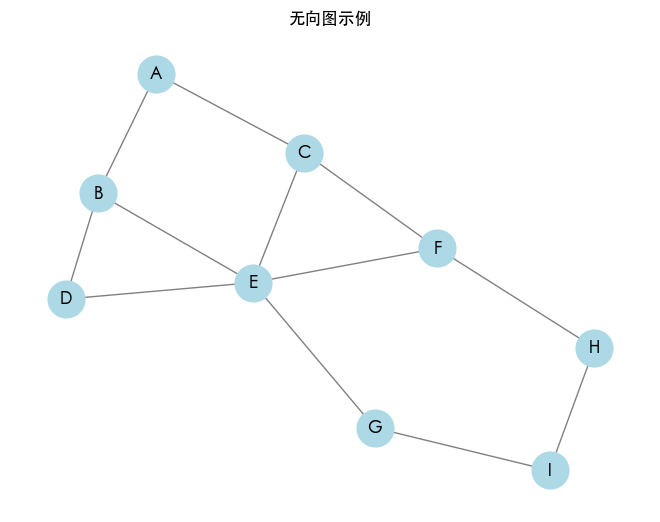
无向图示例

下面是一个无向图示例，适合用于探讨图的遍历（深度优先搜索和广度优先搜索）。

    A
   / \
  B  C
 /|  |
D |  |
 \|  |
  E--F
  |  |
  G  H
   \ |
    I

在这个图中，节点的连接关系如下：

• A 连接 B、C
• B 连接 D、E
• C 连接 E、F
• D 连接 E
• E 连接 G、F
• F 连接 H
• G 连接 I
• H 连接 I

绘制图形

下面的代码使用 networkx 和 matplotlib 库绘制该图。请确保已安装这两个库（如果尚未安装，请运行 pip install networkx matplotlib）。

以下是绘制上述无向图的 Python 代码：

import matplotlib.pyplot as plt
import networkx as nx

# 创建空图
G = nx.Graph()

# 添加节点和边
edges = [
    ('A', 'B'),
    ('A', 'C'),
    ('B', 'D'),
    ('B', 'E'),
    ('C', 'E'),
    ('C', 'F'),
    ('D', 'E'),
    ('E', 'F'),
    ('E', 'G'),
    ('F', 'H'),
    ('G', 'I'),
    ('H', 'I')
]

G.add_edges_from(edges)

# 绘制图形
pos = nx.spring_layout(G)  # 选择布局
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=700, font_size=12, font_weight='bold', edge_color='gray')

# 显示图形
plt.title("无向图示例")
plt.show()

运行上述代码将生成一个表示上述无向图的可视化图形，为后续对深度优先搜索（DFS）和广度优先搜索（BFS）的探讨提供一个演示基础。

代码释意

• 导入库：使用 matplotlib.pyplot 来绘制图形，使用 networkx 来处理图结构。
• 创建图：创建一个无向图对象 G。
• 添加边：通过 add_edges_from 方法将边添加到图中，定义节点之间的连接关系。
• 设置图的布局：使用 spring_layout 选择图形的布局，这有助于更清晰地展示图的结构。
• 绘制图形：使用 nx.draw 来绘制图，设置节点的颜色、大小和标签。
• 显示图：通过 plt.show() 来显示绘制的图形。

深度优先搜索（DFS）

基本概念

深度优先搜索利用栈（可以用递归实现）来访问图中的节点。当访问一个节点时，会深度探索该节点的所有相邻节点，直到无法继续。

算法步骤：

1. 从起始节点开始，标记为已访问。
2. 递归访问未访问的相邻节点。
3. 如果所有相邻节点都已访问，回溯到上一个节点。

下面我们将逐步展示如何使用 Python 代码演示无向图的深度优先搜索（DFS）过程与效果吗，并实现 DFS 算法。

可视化 DFS 过程

在实现 DFS 并打印结果后，我们可以通过 matplotlib 绘制这幅图以可视化 DFS 的遍历过程。为了展示仍然在访问中的节点，我们将在访问每个节点时更新图像。

以下是完整的 DFS 过程可视化实现：

import matplotlib.pyplot as plt
import networkx as nx
import time

class Graph:
    def __init__(self):
        self.graph = nx.Graph()  # 使用 networkx 的 Graph 对象

    def add_edge(self, u, v):
        self.graph.add_edge(u, v)  # 直接添加边到 Graph 对象

    def dfs(self, start):
        visited = set()
        path = []
        self._dfs_util(start, visited, path)
        return path

    def _dfs_util(self, vertex, visited, path):
        visited.add(vertex)
        path.append(vertex)  # 记录路径
        self.visualize_dfs(path)  # 可视化图遍历
        for neighbor in self.graph[vertex]:  # 使用 networkx 的方式访问相邻节点
            if neighbor not in visited:
                self._dfs_util(neighbor, visited, path)

    def visualize_dfs(self, path):
        plt.clf()  # 清空当前的图
        pos = nx.spring_layout(self.graph)
        nx.draw(self.graph, pos, with_labels=True, node_color='lightblue', node_size=700, font_size=12, font_weight='bold', edge_color='gray')
        # 着色已访问的节点
        nx.draw_networkx_nodes(self.graph, pos, nodelist=path, node_color='orange')
        plt.title("深度优先搜索（DFS）可视化")
        plt.pause(0.5)  # 暂停以绘制图像


# 创建无向图
G = Graph()
edges = [
    ('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'),
    ('C', 'E'), ('C', 'F'), ('D', 'E'), ('E', 'F'),
    ('E', 'G'), ('F', 'H'), ('G', 'I'), ('H', 'I')
]

for u, v in edges:
    G.add_edge(u, v)

# 设置图的布局
plt.ion()  # 开启交互模式
plt.figure(figsize=(8, 6))

# 执行 DFS
dfs_result = G.dfs('A')
print("深度优先搜索的结果:", dfs_result)

plt.ioff()  # 关闭交互模式
plt.show()  # 显示最终图
# 深度优先搜索的结果: ['A', 'B', 'D', 'E', 'C', 'F', 'H', 'I', 'G']

代码释意

• 图的构建：使用 add_edge 方法构建无向图，确保每个节点都相互连接。
• DFS 实现：使用递归方法进行深度优先搜索，同时在每次访问节点时调用可视化函数。
• 可视化函数：使用 matplotlib 不断更新图的显示，以展示各个节点的遍历状态。
• 交互模式：通过开启交互模式（plt.ion()），允许我们逐步更新图。

运行示例

运行上面的完整代码，可以看到图的遍历过程。每次访问一个节点时，节点将会变为橙色，表示已访问。最终，程序也会打印出 DFS 的结果路径。

深度优先搜索的结果: ['A', 'B', 'D', 'E', 'C', 'F', 'H', 'I', 'G']

深度优先搜索（DFS）

下面是 DFS 算法的实现。我们使用一个递归方法进行实现，在访问每个节点时记录路径，以便可视化图遍历结果。

import matplotlib.pyplot as plt
import networkx as nx

class Graph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        if v not in self.graph:
            self.graph[v] = []
        self.graph[u].append(v)
        self.graph[v].append(u)  # 无向图，双向添加

    def dfs(self, start):
        visited = set()
        path = []
        self._dfs_util(start, visited, path)
        return path

    def _dfs_util(self, vertex, visited, path):
        visited.add(vertex)
        path.append(vertex)  # 记录路径
        for neighbor in self.graph.get(vertex, []):
            if neighbor not in visited:
                self._dfs_util(neighbor, visited, path)

# 创建无向图
G = Graph()
edges = [
    ('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'),
    ('C', 'E'), ('C', 'F'), ('D', 'E'), ('E', 'F'),
    ('E', 'G'), ('F', 'H'), ('G', 'I'), ('H', 'I')
]

for u, v in edges:
    G.add_edge(u, v)

# 执行 DFS
dfs_result = G.dfs('A')
print("深度优先搜索的结果:", dfs_result)
# 深度优先搜索的结果: ['A', 'B', 'D', 'E', 'C', 'F', 'H', 'I', 'G']

关键点

• 递归深度：DFS 的递归深度可能导致栈溢出，特别是在具有深层嵌套的图上。可考虑使用显式栈来替代递归。
• 访问状态：使用集合来管理访问状态，提高查询效率。

DFS 应用场景

• 连通性检测：判断图中是否存在连接路径。
• 图的遍历：访问图中的所有节点。
• 找出图中的环：通过深度优先遍历可以判断图中是否存在环。
• 路径查找：在特定情况下寻找从起点到终点的路径。

广度优先搜索（BFS）

基本概念

广度优先搜索利用队列来逐层访问图中的节点。首先访问起始节点，然后将所有直接相邻的节点入队，并继续出队和访问这些节点。

算法步骤：

1. 从起始节点开始，将其加入队列并标记为已访问。
2. 循环直到队列为空，出队当前节点，并访问其相邻节点。
3. 将未访问的相邻节点入队并标记为已访问。

我们逐步展示如何使用 Python 代码演示无向图的广度优先搜索（BFS）过程与效果，以及实现 BFS 算法。

可视化 BFS 过程

以下是使用队列实现 BFS，访问每个节点时记录路径，以及可视化图遍历结果。

import matplotlib.pyplot as plt
import networkx as nx
from collections import deque

class Graph:
    def __init__(self):
        self.graph = nx.Graph()  # 使用 networkx 的 Graph 对象

    def add_edge(self, u, v):
        self.graph.add_edge(u, v)  # 直接添加边到 Graph 对象

    def bfs(self, start):
        visited = set()
        path = []
        queue = deque([start])  # 使用 deque 作为队列

        while queue:
            vertex = queue.popleft()
            if vertex not in visited:
                visited.add(vertex)
                path.append(vertex)  # 记录路径
                self.visualize_bfs(path)  # 可视化图遍历
                for neighbor in self.graph[vertex]:
                    if neighbor not in visited:
                        queue.append(neighbor)  # 将未访问的相邻节点加入队列

        return path

    def visualize_bfs(self, path):
        plt.clf()  # 清空当前的图
        pos = nx.spring_layout(self.graph)
        nx.draw(self.graph, pos, with_labels=True, node_color='lightblue', node_size=700, font_size=12, font_weight='bold', edge_color='gray')
        # 着色已访问的节点
        nx.draw_networkx_nodes(self.graph, pos, nodelist=path, node_color='orange')
        plt.title("广度优先搜索（BFS）可视化")
        plt.pause(0.5)  # 暂停以绘制图像

# 创建无向图
G = Graph()
edges = [
    ('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'),
    ('C', 'E'), ('C', 'F'), ('D', 'E'), ('E', 'F'),
    ('E', 'G'), ('F', 'H'), ('G', 'I'), ('H', 'I')
]

for u, v in edges:
    G.add_edge(u, v)

# 设置图的布局
plt.ion()  # 开启交互模式
plt.figure(figsize=(8, 6))

# 执行 BFS
bfs_result = G.bfs('A')
print("广度优先搜索的结果:", bfs_result)

plt.ioff()  # 关闭交互模式
plt.show()  # 显示最终图

代码释意

• Graph 类：
  • 使用 nx.Graph() 创建无向图。
  • add_edge(u, v) 方法将边添加到图中。
• 广度优先搜索（BFS）：
  • bfs(start) 方法使用队列（deque）遍历图。
  • 访问每个节点时，将其添加到路径中，并调用 visualize_bfs() 方法进行图的可视化。
• 可视化方法：
  • visualize_bfs(path) 方法清空图并重新绘制，只标记已访问的节点。
  • 使用 plt.pause(0.5) 使图的更新可见。

运行示例

运行上述代码后，将看到一个窗口，展示 BFS 的遍历过程。每次访问一个节点时，该节点会变为橙色，同时终端将打印 BFS 的结果路径。

广度优先搜索的结果: ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']

广度优先搜索（BFS）

以下是 BFS 的实现示例：

from collections import deque

class Graph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        self.graph[u].append(v)

    def bfs(self, start):
        visited = set()
        queue = deque([start])
        visited.add(start)

        while queue:
            vertex = queue.popleft()
            print(vertex)  # 处理节点
            for neighbor in self.graph.get(vertex, []):
                if neighbor not in visited:
                    visited.add(neighbor)
                    queue.append(neighbor)

# 示例
g = Graph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
g.add_edge(2, 5)

print("广度优先搜索（BFS）结果：")
g.bfs(0)
# 广度优先搜索（BFS）结果：
# 0
# 1
# 2
# 3
# 4
# 5

关键点

• 队列管理：使用双端队列（deque）提高入队和出队效率。
• 内存消耗：BFS 可能在大图上消耗更多的内存，以存储队列和访问状态。

应用场景

• 最短路径查找：在无权图中，BFS 可找到从源节点到其他节点的最短路径。
• 网络广播：在网络中实现信息传播。
• 连通分量的寻找：用于找出不同的连通区域。

DFS vs. BFS

深度优先搜索（DFS）和广度优先搜索（BFS）是图遍历的两种基本算法，各自具有独特的特点和应用场景。

基本概念对比

DFS 尽可能深地搜索图的分支，直到该分支末端才会进行回溯。可以基于递归或显式栈来实现。沿着一条路径走到尽头，再回退到最近的分支。

BFS 按层次逐层扩展，同一层的节点会在深入下一层之前全部访问。使用队列来实现。首先访问起点的所有直接邻居，然后依次访问每个邻居的邻居，直到所有节点被访问。

性能对比

• 时间复杂度：
  • DFS：O(V + E) \，$V$ 是顶点数，$E$ 是边数。
  • BFS：$O(V + E)$，同样的复杂度。
• 空间复杂度：
  • DFS：最坏情况下为 $O(h)$，$h$ 是树的高度（对于深度较大的图可能会出现栈溢出）。
  • BFS：最坏情况下为 $O(V)$，因为可能需要存储所有节点。

场景分析

深度优先搜索（DFS）

• 应用领域：
  • 图的连通性检测：DFS 可以用来检测图是否连通，或找到图的连通分量。
  • 路径查找：适合查找从起点到终点的任意路径（不是最短路径）。
  • 拓扑排序：在有向无环图（DAG）中进行拓扑排序。
  • 拼图游戏：如八数码问题、迷宫求解等可以使用 DFS 来尝试不同路径。
• 场景示例：
  • 迷宫探索：在迷宫中寻找一条通向出口的路径，DFS 可以快速深入复杂的路径。
  • 网络爬虫：在网页链接中递归访问，直到没有未访问的链接。

广度优先搜索（BFS）

• 应用领域：
  • 最短路径查找：BFS 可以在无权图中找到从起点到终点的最短路径。
  • 层次遍历：适合在树或图中进行层次遍历，获取节点的层级信息。
  • 网络广播：在传播消息或数据时使用 BFS，有助于确保信息的快速扩散。
• 具体示例：
  • 社交网络分析：在社交网络中查找用户之间的最短连接。
  • 路径规划：如地图中的最短路径规划，帮助导航。

总结对比

特点	深度优先搜索（DFS）	广度优先搜索（BFS）
主要策略	深度优先，不回头	层次优先
实现方式	递归或栈	队列
应用场景	路径搜索、拓扑排序、迷宫	最短路径、网络传播
时间复杂度	$O(V + E)$	$O(V + E)$
空间复杂度	$O(h)$	$O(V)$

在实际问题中，根据具体需求选择最合适的算法：如果需求是查找最短路径，尤其是在无权图中，选择 BFS。如果需要探索所有可能的路径或解决递归问题，使用 DFS。选择合适的遍历方法能提高解决问题的效率和有效性。

社交网络图遍历

假设在一个社交网络中，我们想要找到从用户 A 出发能到达的所有用户，并且希望探索社交网络的至少一层。

• 输入：用户 A 的 ID， 一个社交网络图。
• 目标：获取从用户 A 出发的所有直接联系人和关系。

我们可以针对这个问题分别使用 DFS 和 BFS。

使用 DFS

# DFS 实现
g = Graph()
g.add_edge('A', 'B')
g.add_edge('A', 'C')
g.add_edge('B', 'D')
g.add_edge('B', 'E')
g.add_edge('C', 'F')

print("DFS 结果：")
g.dfs('A')

输出将是：

A
B
D
E
C
F

使用 BFS

# BFS 实现
g = Graph()
g.add_edge('A', 'B')
g.add_edge('A', 'C')
g.add_edge('B', 'D')
g.add_edge('B', 'E')
g.add_edge('C', 'F')

print("BFS 结果：")
g.bfs('A')

输出将是：

A
B
C
D
E
F

结语

通过深度优先搜索（DFS）和广度优先搜索（BFS）两种图遍历方法，我们能够有效地解决多种图论问题。根据不同需求选择正确的遍历方式，当需要寻找图中的所有路径或连通分量时，或处理树结构上的递归问题时，DFS 是一个不错的选择。而当需要寻找最短路径或进行层次遍历时，BFS 是更好的选择。

在实际应用中，评估图的特性和需求，从而选择最合适的遍历方法是极其重要的。此外，应合理管理内存使用，避免栈溢出和内存消耗过高等问题。

---

PS：感谢每一位志同道合者的阅读，欢迎关注、点赞、评论！