跳到主要内容

模型训练

信息
2023年12月4日 · · · 阅读需 33 分钟

在训练不同机器学习算法模型时，遇到的各类训练算法大多对用户都是一个黑匣子，而理解它们实际怎么工作，对用户是很有帮助的；

  • 快速定位到合适的模型与正确的训练算法，找到一套适当的超参数等；
  • 更高效的执行错误调试、错误分析等；
  • 有助于理解、构建和训练神经网络等；

训练方法

  • 线性回归模型
    • 闭式方程，直接计算出最拟合训练集的模型参数（使训练集上的成本函数最小化的模型参数）；
    • 迭代优化（GD、梯度下降、梯度下降变体、小批量梯度下降、随机梯度下降），逐渐调整模型参数直至训练集上的成本函数调至最低；
  • 多项式回归模型
    • 学习曲线评估过拟合情况
    • 正则化技巧（降低过拟合风险）
  • 分类模型
    • Logistic 回归
    • Softmax 回归

1. 线性回归​

线性模型可以当做是对输入特征做加权求和，再加上一个偏置项（截距项）常数；

线性回归模型预测

y^=θ0+θ1x1+θ2x2+...+θnxn \hat{y} = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n
  • y^\hat{y}，预测值；
  • n，特征数量；
  • xix_i，第 i 个特征值；
  • θj\theta_j，第 j 个模型参数（包括偏差项 θ0\theta_0 和特征权重 θ1\theta_1、θ2\theta_2、...、θn\theta_n）；

线性回归模型预测（向量化形式）

y^=hθ(x)=θ⋅x \hat{y} = h_\theta(x) = \theta · x
  • θ\theta，模型的参数向量，其中包含偏差项 θ0\theta_0 和特征权重 θ1\theta_1 至 θn\theta_n
  • x，实例的特征向量，包含从 x0x_0 到 xnx_n, x0x_0 始终等于 1；
  • θ⋅x\theta · x，向量 θ\theta 和 X 的点积，它相当于 θ0x0+θ1x1+θ2x2+...+θnxn\theta_0x_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n；
  • hθh_\theta，假设函数，使用模型参数 θ\theta；

特征向量（feature vector），一个样本对应在样本空间中坐标轴上的坐标向量； 向量，在机器学习中通常表示列向量，表示单一列的二维数组；

线性回归模型的 MSE 成本函数

MSE=(X,hθ)=1m∑i=1m(θTx(i)−y(i))2 MSE = (X, h_\theta) = \frac{1}{m}\sum_{i=1}^m(\theta^Tx^{(i)} - y^{(i)})^2
  • hθh_\theta，其中的 θ\theta 表示模型 h 是被向量 θ\theta 参数化的；

1. 标准方程​

  • 闭式解方法，直接得出使成本函数最小的 θ\theta 值的数据方程，也称标准方程；
θ^=(XTX)−1XTy \hat{\theta} = (X^TX)^{-1}X^Ty
  • θ^\hat{\theta}，使成本函数最小的 θ\theta 值；
  • y，包含 y(1)y^{(1)} 到 y(m)y^{(m)} 的目标值向量；

使用线性数据测试标准方程

import numpy as np

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()

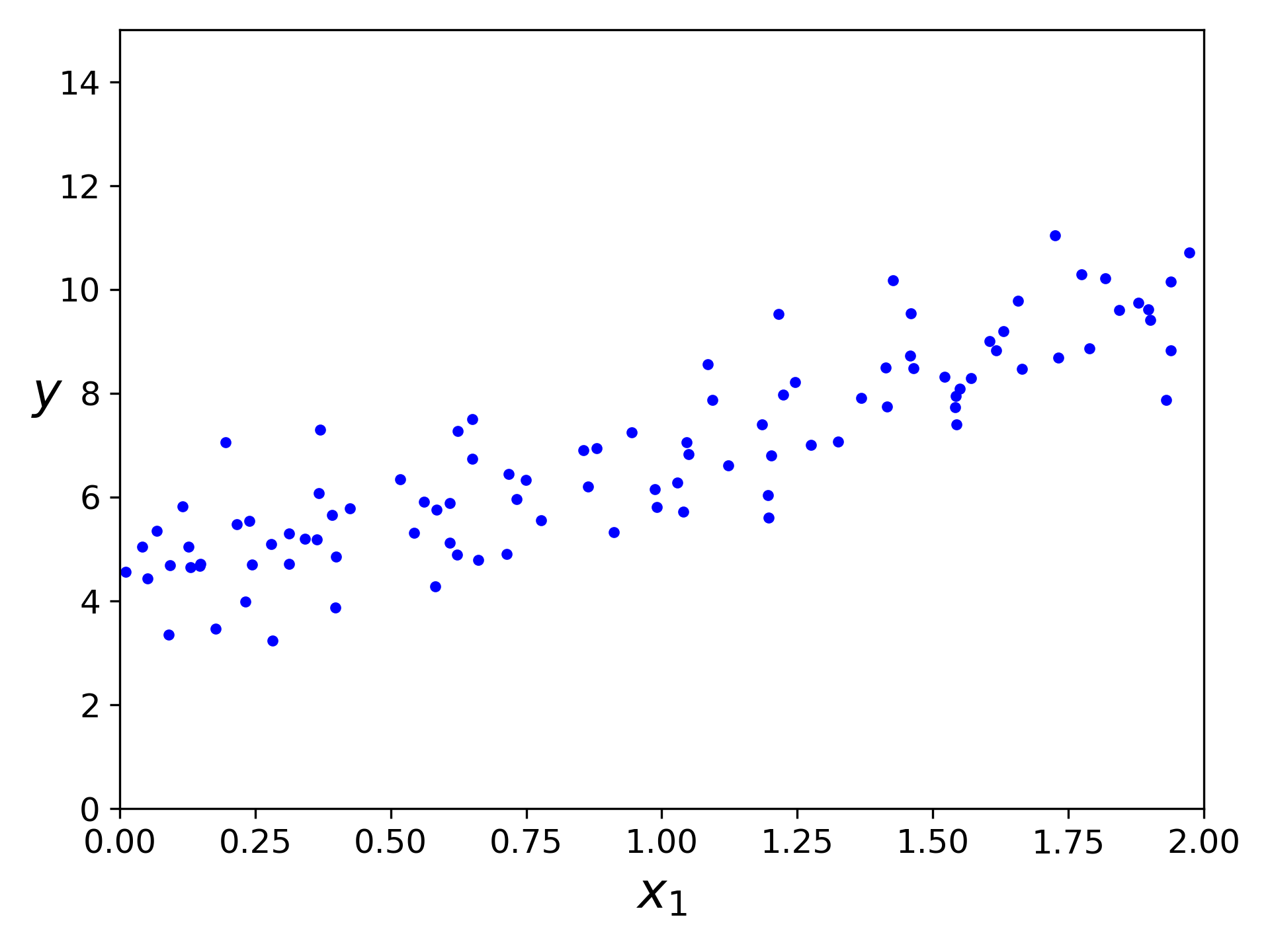
generated data plot

使用标准方程计算 θ^\hat{\theta}

  • inv()，对矩阵求逆；
  • dot()，计算矩阵的内积；
>>> X_b = np.c_[np.ones((100, 1)), X]  # add x0 = 1 to each instance
>>> theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
>>>
array([[4.21509616],
       [2.77011339]])

原本的 θ0\theta_0=4，θ1\theta_1=3，这里算出的 θ0\theta_0=4.215，θ1\theta_1=2.770，已经比较接近；

使用 θ^\hat{\theta} 做预测

>>> X_new = np.array([[0], [2]])
>>> X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance
>>> y_predict = X_new_b.dot(theta_best)
>>> y_predict
array([[4.21509616],
       [9.75532293]])

绘制模型的预测结果

plt.plot(X_new, y_predict, "r-", linewidth=2, label="Predictions")
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 2, 0, 15])
plt.show()

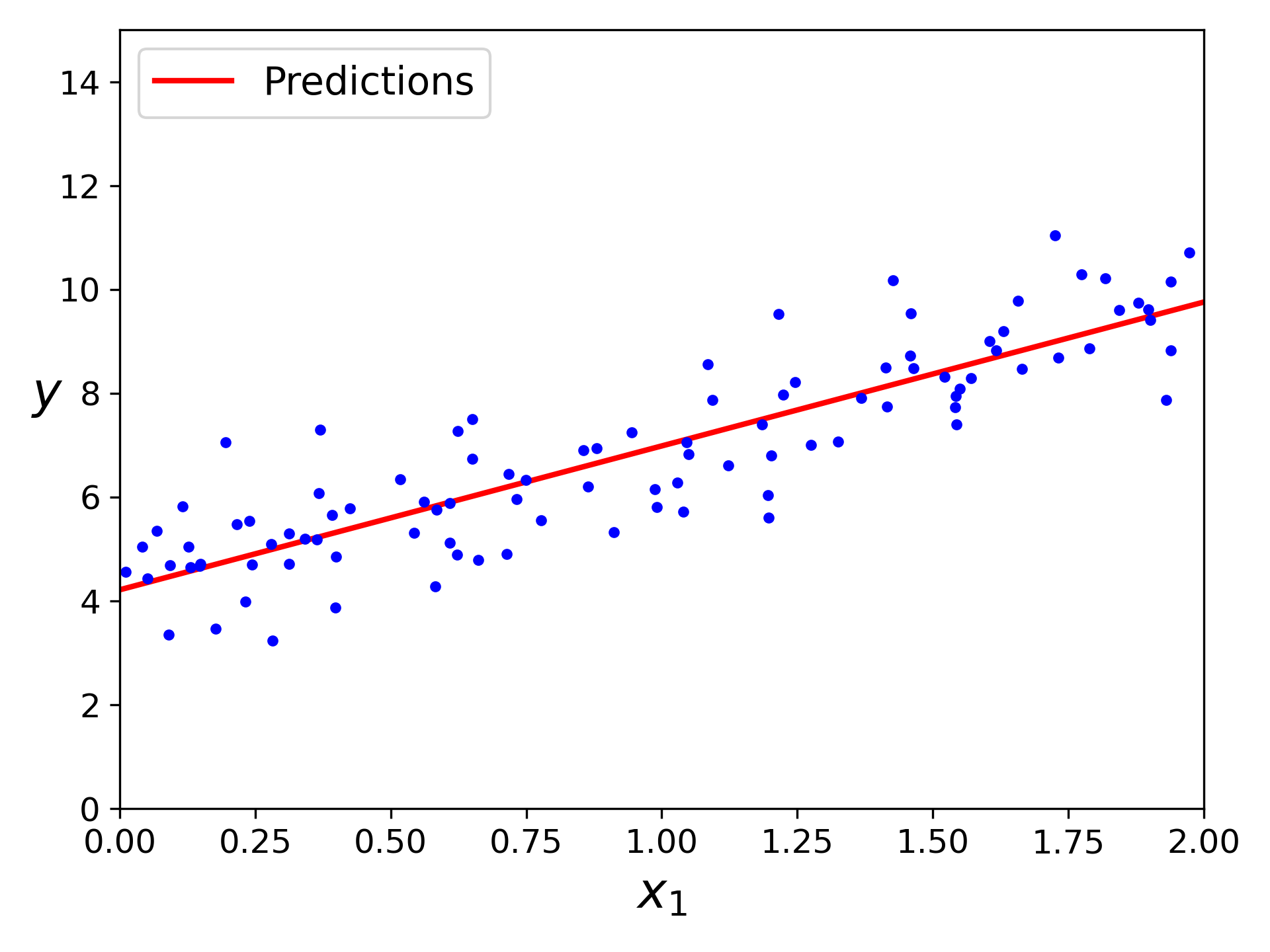
linear model predictions plot

2. 奇异值分解​

回顾使用 Scikit-Learn 的 LinearRegression

>>> from sklearn.linear_model import LinearRegression
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X, y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([4.21509616]), array([[2.77011339]]))
>>> lin_reg.predict(X_new)
array([[4.21509616],
       [9.75532293]])
  • intercept_，偏差项；
  • coef_，特征权重；

LinearRegression 的 θ\theta 是基于 scipy.linalg.lstsq() 函数（最小二乘）计算的；

θ^=X+y \hat{\theta} = X^{+}y
  • X+X^{+}，X 的伪逆；
>>> theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
>>> theta_best_svd
array([[4.21509616],
       [2.77011339]])

使用 np.linalg.pinv() 计算伪逆

>>> np.linalg.pinv(X_b).dot(y)
array([[4.21509616],
       [2.77011339]])
  • 奇异值分解（Singular Value Decomposition，SVD），计算伪逆的标准矩阵分解技术，可将训练集矩阵 X 分解成三个矩阵 U∑VTU\sum{}V^{T} 的乘积（numpy.linalg.svd() 实现）；
X+=V∑+UT X^{+} = V\sum{}^{+}U^{T}
  • ∑+\sum^{+} 的计算方式：取 ∑\sum 并将所有小于一个阈值的值设置成 0，再将非 0 值替换成它们的倒数，最后把结果矩阵转置；

** SVD vs. 标准方程**

伪逆比标准方程更有效，可以很好的处理边缘问题，若 XTXX^TX 是不可逆的，标准方程可能无解，而伪逆总是有定义的；

3. 计算复杂度​

标准方程相对特征数量 n 的计算复杂度

O(n2.4)−>O(n3) O(n^{2.4}) -> O(n^{3})

标准方程计算的是 XTXX^{T}X 的逆，XTXX^{T}X 是一个 (n+1)×(n+1)(n+1) \times (n+1) 的矩阵（n 是特征数），求逆的计算复杂度通常为 O(n2.4)O(n^{2.4}) 至 O(n3)O(n^{3})（具体取决于实现方式）；当 n 翻倍，计算复杂度将变大 22.42^{2.4}=5.3 至 232^3=8 倍；

SVD 相对特征数量 n 的计算复杂度

O(n2)O(n^2)

相对于训练集的实例数量 O(m)O(m)，标准方程和 SVD 的计算复杂度都是线性的；

线性回归模型一经训练（不论标准方程还是其他算法），预测就非常快，计算复杂度相对于要预测实例数量和特征数量都是线性的；

2. 梯度下降​

假设你迷失在山上的浓雾之中，你能感觉到的只有你脚下路面的坡度；快速到达山脚的一个策略就是沿着最陡的方向下坡；

  • 梯度下降算法，通过测量参数向量 θ\theta 相关的误差函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为 0，达到最小值；

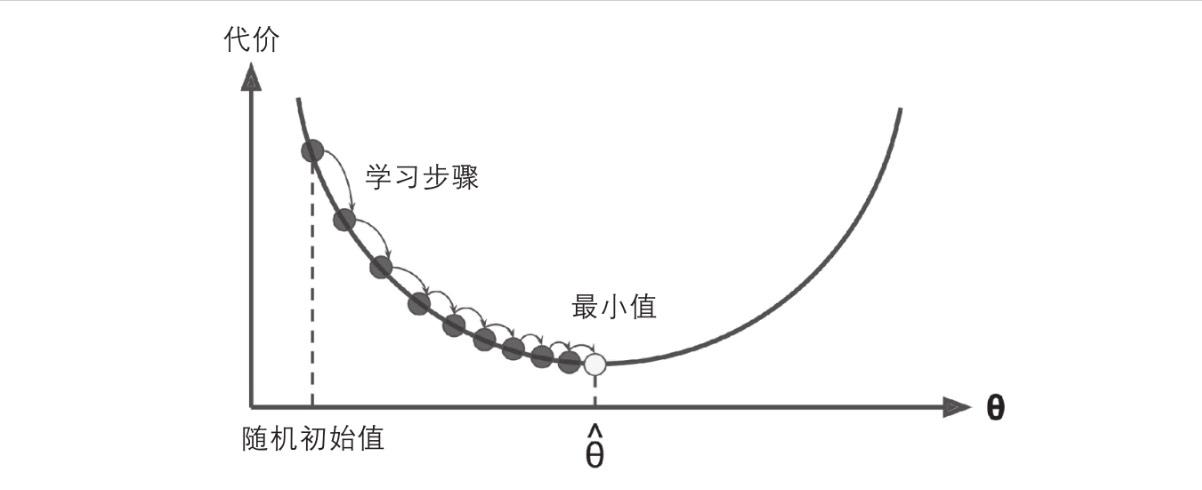
梯度下降过程

首先随机选择一个 θ\theta 值（随机初始化），然后逐步改进，每次踏出一步，每步参试降低一点成本函数（如 MSE），直到算法收敛为一个最小值；

  • 学习率，超参数，梯度下降每一步的步长；
    • 太低，算法需要大量迭代才能收敛，耗时变得很长；
    • 太高，导致算法发散，值越来越大，可能直接越过山谷到达另一边，甚至比之前的起点还高，无法找到最优解；

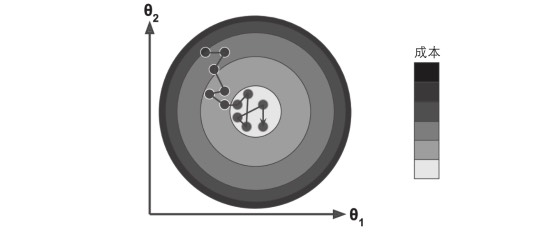
梯度下降陷阱

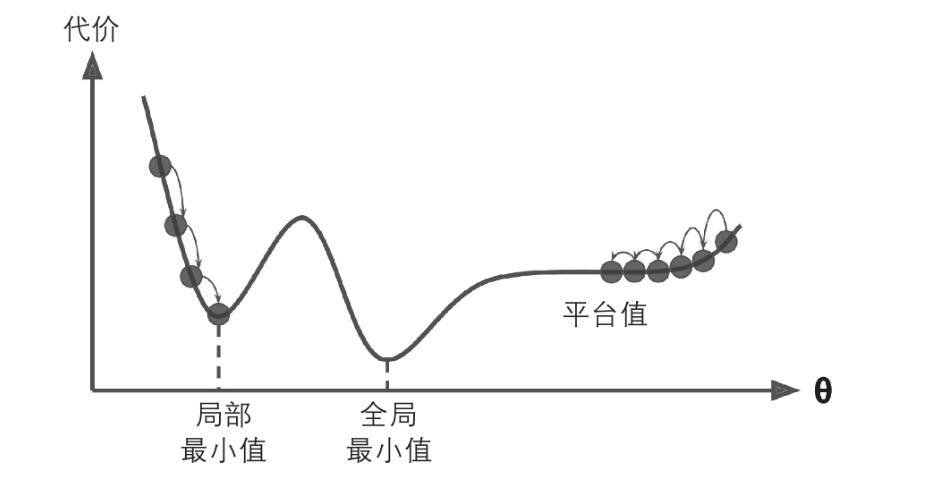
梯度下降陷阱

并非所有的成本函数都是一个碗型的，可能如图一般不规则，导致很难收敛到全局最小值；若随机初始化起点在左侧，会收敛到一个局部最小值，而非全局最小值；若随机初始化起点在右侧，则可能需要很长一段时间才能迭代到最低点，若停下得太早，可能永远无法到底全局最小值；

线性回归模型的 MSE 成本函数是一个连续的凸函数，因此不存在局部最小值，只有一个全局最小值，且斜率不会产生陡峭变化；即使乱走梯度下降也可以趋近全局最小值；

细长碗状成本函数

因不同特征的尺寸差异巨大导致的细长碗状成本函数；特征值越小（如 θ1\theta_1），就需要更大的变化来影响成本函数；

梯度下降成本（细长碗状）

左图的梯度下降算法直接走向最小值，可以快速到达；右图则先沿着与全局最小值方向近乎垂直的方向前进，然后验证近乎平坦的山谷走到最小值，需要花费大量时间；

应用梯度下降时，需保证所有特征值大小比例相差不多（比如使用 Scikit-Learn 的 StandardScaler），否则收敛时间会长很多；

训练模型也就是搜寻使成本函数（在训练集上）最小化的参数组合；这是模型参数空间层面上的搜索，模型的参数越多，这个空间的维度就越多，搜索就越难；同样是在干草堆里寻找一根针，在一个三百维的空间里就比在一个三维空间里要棘手得多；幸运的是，线性回归模型的成本函数是凸函数，针就躺在碗底；

1. 批量梯度下降​

实现梯度下降需要计算每个模型关于参数 θj\theta_j 的成本函数的梯度，即计算关于参数 θj\theta_j 的成本函数的偏导数，计作 ∂∂θjMSE(θ)\frac{\partial}{\partial\theta_j}MSE(\theta)；

成本函数的偏导数

∂∂θjMSE(θ)=2m∑i=1m(θTx(i)−y(i))xj(i) \frac{\partial}{\partial\theta_j}MSE(\theta) = \frac{2}{m}\sum_{i=1}^{m}(\theta^{T}x^{(i)} - y^{(i)})x_j^{(i)}

一次性计算偏导数

▽θMSE(θ)=(∂∂θ0MSE(θ)∂∂θ1MSE(θ)...∂∂θnMSE(θ)) =2mXT(Xθ−y) \triangledown_\theta MSE(\theta) = \begin{pmatrix} \frac{\partial}{\partial\theta_0}MSE(\theta) \\ \frac{\partial}{\partial\theta_1}MSE(\theta) \\ ... \\ \frac{\partial}{\partial\theta_n}MSE(\theta) \\ \end{pmatrix} \ = \frac{2}{m} X^{T}(X\theta - y)

在计算梯度下降的每一步时，都是基于完整的训练集 X 的；因此面对非常庞大的训练集时，算法会变得极慢（梯度下降算法随特征数量扩展的表现比较好，比如几十万个特征，梯度下降比标准方程或者 SVD 要快很多）；

梯度下降步骤

θ(next)=θ−η▽θMSE(θ) \theta^{(next)} = \theta - \eta \triangledown_\theta MSE(\theta)
  • η\eta，学习率，用梯度向量乘以 η\eta 确定下坡步长的大小；

梯度下降的快速实现

eta = 0.1  # learning rate
n_iterations = 1000
m = 100

theta = np.random.randn(2, 1)  # random initialization

for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
    theta = theta - eta * gradients

print(theta)
[[4.21509616]
 [2.77011339]]

theta 计算结果与标准方程的计算结果相同；

计算三种学习率的梯度下降前十步

虚线表示起点；

theta_path_bgd = []

def plot_gradient_descent(theta, eta, theta_path=None):
    m = len(X_b)
    plt.plot(X, y, "b.")
    n_iterations = 1000
    for iteration in range(n_iterations):
        if iteration < 10:
            y_predict = X_new_b.dot(theta)
            style = "b-" if iteration > 0 else "r--"
            plt.plot(X_new, y_predict, style)
        gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
        theta = theta - eta * gradients
        if theta_path is not None:
            theta_path.append(theta)
    plt.xlabel("$x_1$", fontsize=18)
    plt.axis([0, 2, 0, 15])
    plt.title(r"$\eta = {}$".format(eta), fontsize=16)

np.random.seed(42)
theta = np.random.randn(2,1)  # random initialization

plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
plt.show()

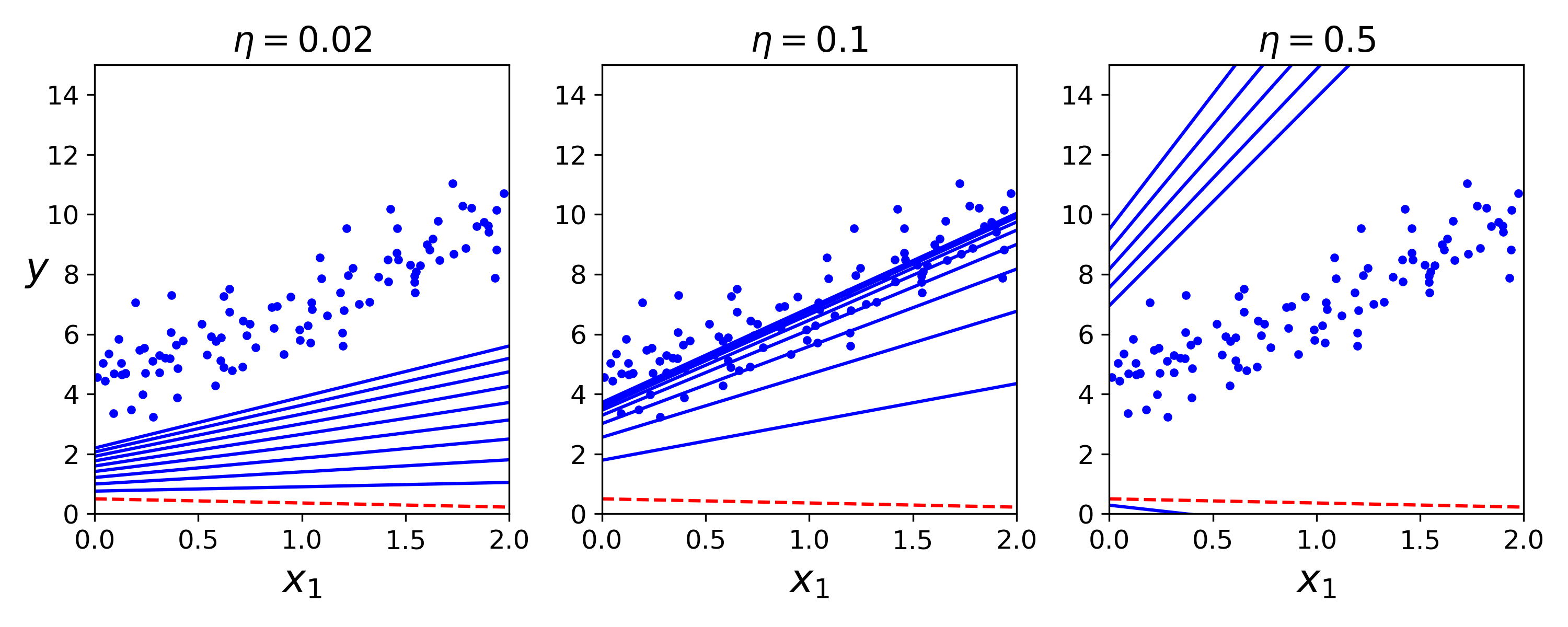
gradient descent plot

  • 左图，学习率太低，需要太长时间找到解决方法；
  • 中图，学习率恰好，经过几次迭代收敛出了最终解；
  • 右图，学习率太高，算法发散，直接跳过了数据区域，且每次都离实际解决方案越来越远；

可以通过网格搜索找到合适的学习率，但需要限制迭代次数从而淘汰掉那些收敛耗时太长的模型；

  • 限制迭代次数的简单办法是，在开始时设置一个非常大的迭代次数，当梯度向量的值变得非常微小时中断；即当梯度向量的范数变得低于容差时，梯度下降到了几乎最小值；

  • 收敛速度，若成本函数为凸函数，且斜率没有陡峭变化（如 MSE 的成本函数），则具有固定学习率的批量梯度下降最终会收敛到最佳解；若将容差缩小到原来的 1/10 以得到更精确的解，算法将不得不运行 10 倍的时间；

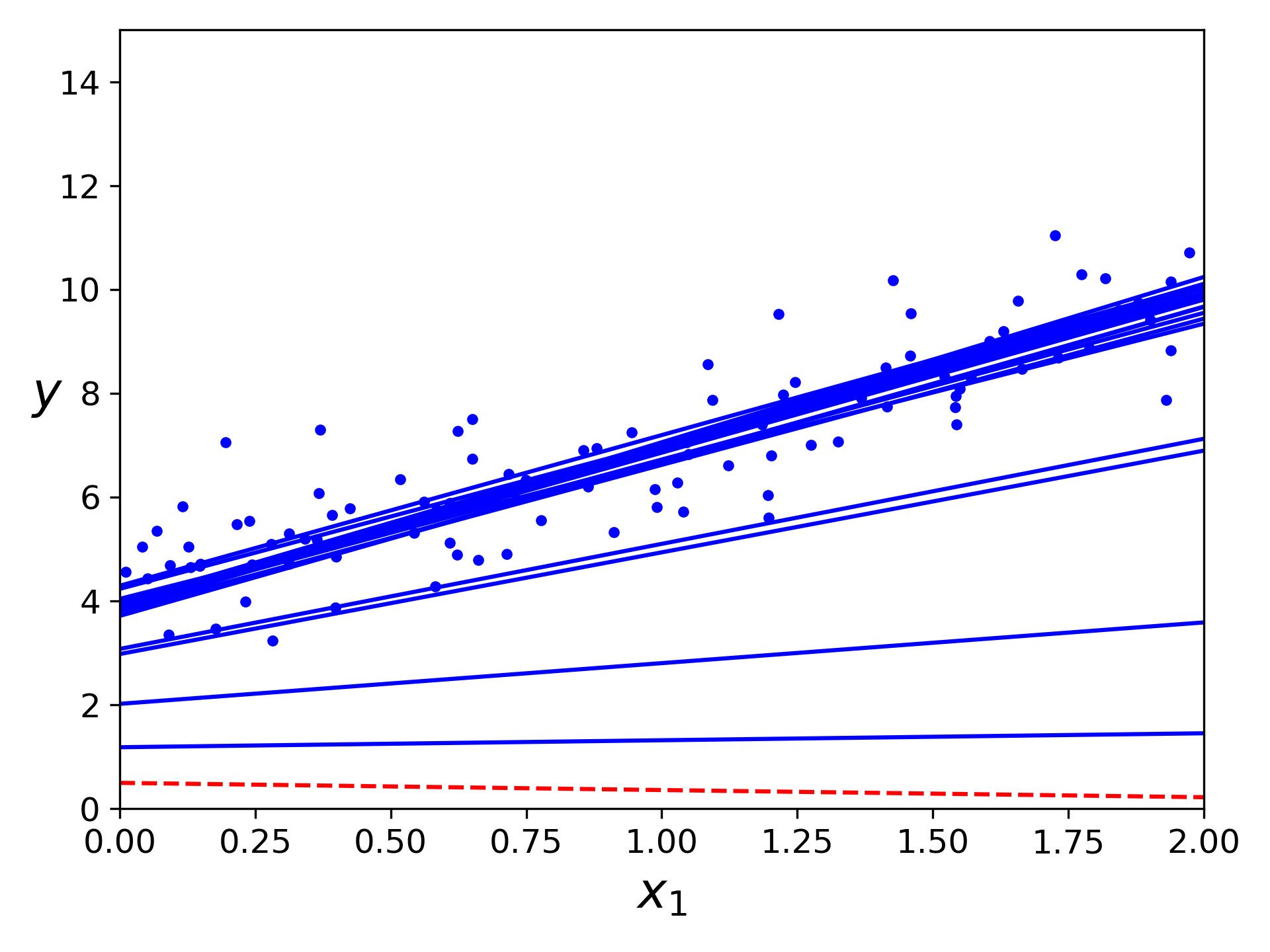
2. 随机梯度下降​

  • 随机梯度下降，与使用整个训练集计算每一步的梯度，算法特别慢的批量梯度下降相对，随机梯度下降在每一步梯度计算时，在训练集随机选择一个实例计算梯度，算法很快；可用于海量数据集的训练，每次迭代只需要在内存中运行一个实例（SGD 可以作为核外算法实现）；

随机梯度下降训练过程

随机梯度下降的随机性质让它比批量梯度下降要不规则得多；成本函数不再是持续下降至最下值，而是存在上下波动，但整体上会慢慢下降，最终接近最小值（即时达到最小值依旧会反弹，该算法的参数值只能是足够好，不会是最优）；

  • 逃离局部最优，成本函数非常不规则时，随机梯度下降可以跳出局部最小值，相比批量梯度下降，它更能找到全局最小值；

  • 模拟退火，逐步降低学习率，开始的步长较大，快速进展和逃离局部最小值，然后越来越小，让算法尽量靠近全局最小值；

  • 学习率调度，确认每个迭代学习率的函数；

学习率降得太快可能陷入局部最小值，学习率降得太慢可能需要太长时间走到最小值的附近，提前结束训练可能导致得到一个次优的解决方案；

学习率调度实现随机梯度下降

theta_path_sgd = []
m = len(X_b)
np.random.seed(42)

n_epochs = 50
t0, t1 = 5, 50  # learning schedule hyperparameters


def learning_schedule(t):
    return t0 / (t + t1)


theta = np.random.randn(2, 1)  # random initialization

for epoch in range(n_epochs):
    for i in range(m):
        if epoch == 0 and i < 20:
            y_predict = X_new_b.dot(theta)
            style = "b-" if i > 0 else "r--"
            plt.plot(X_new, y_predict, style)
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients
        theta_path_sgd.append(theta)

plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()

sgd plot

随机选取事例，某些实例可能每个轮次被选中多次，有的实例则可能不会被选中；

  • IID，独立且均匀分布，在训练过程中对实例进行随机混洗；使用随机梯度下降时，训练实例必须独立且均匀分布，确保平均而言将参数拉向全局最优值；
>>> print(theta)
[[4.21076011]
 [2.74856079]]

使用 SGDRegressor 执行线性回归

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())

print(sgd_reg.intercept_, sgd_reg.coef_)
[4.22520079] [2.79873691]
  • max_iter，最多可运行的轮次数；
  • tol，轮次期间损失下降小于该值将停止训练；
  • eta0，起始学习率；

3. 小批量梯度下降​

  • 小批量梯度下降，相比于基于完整训练集（如批量梯度下降）和基于一个实例（如随机梯度下降）来计算梯度，小批量梯度下降在小型批量的随机实例集上计算梯度；可以通过矩阵操作的硬件优化（如 GPU）来提高性能；

小批量梯度下降比随机梯度下降在参数空间上的进展更稳定，且最终更接近最小值，但可能很难摆脱局部最小值（局部最小值影响情况下不像线性回归）；而批量梯度下降最终会实际停留在最小值，只是批量梯度下降每一步需要花费很多时间；好的处理方式是使用良好的学习率调度让随机梯度下降和小批量梯度下降尽可能达到最小值；

线性回归算法的比较

算法m 很大核外支持n 很大超参数要求缩放Scikit-Learn
标准方程快否慢0否N/A
SVD快否慢0否LinearRegression
批量 GD慢否快2是SGDRegressor
随机 GD快是快>= 2是SGDRegressor
小批量 GD快是快>= 2是SGDRegressor

所有这些算法最终都具有非常相似的模型，且以完全相同的方式进行预测；

3. 多项式回归​

  • 多项式回归，使用线性模型来拟合非线性模型；比如将每个特征的幂次方添加为一个新特征，然后在此扩展特征集上训练一个线性模型；

多项式回归示例：y=ax2+bx+cy=ax^2+bx+c

在二次方程 y=ax2+bx+cy=ax^2+bx+c 的基础上添加一些噪声；

np.random.seed(42)

m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)

plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()

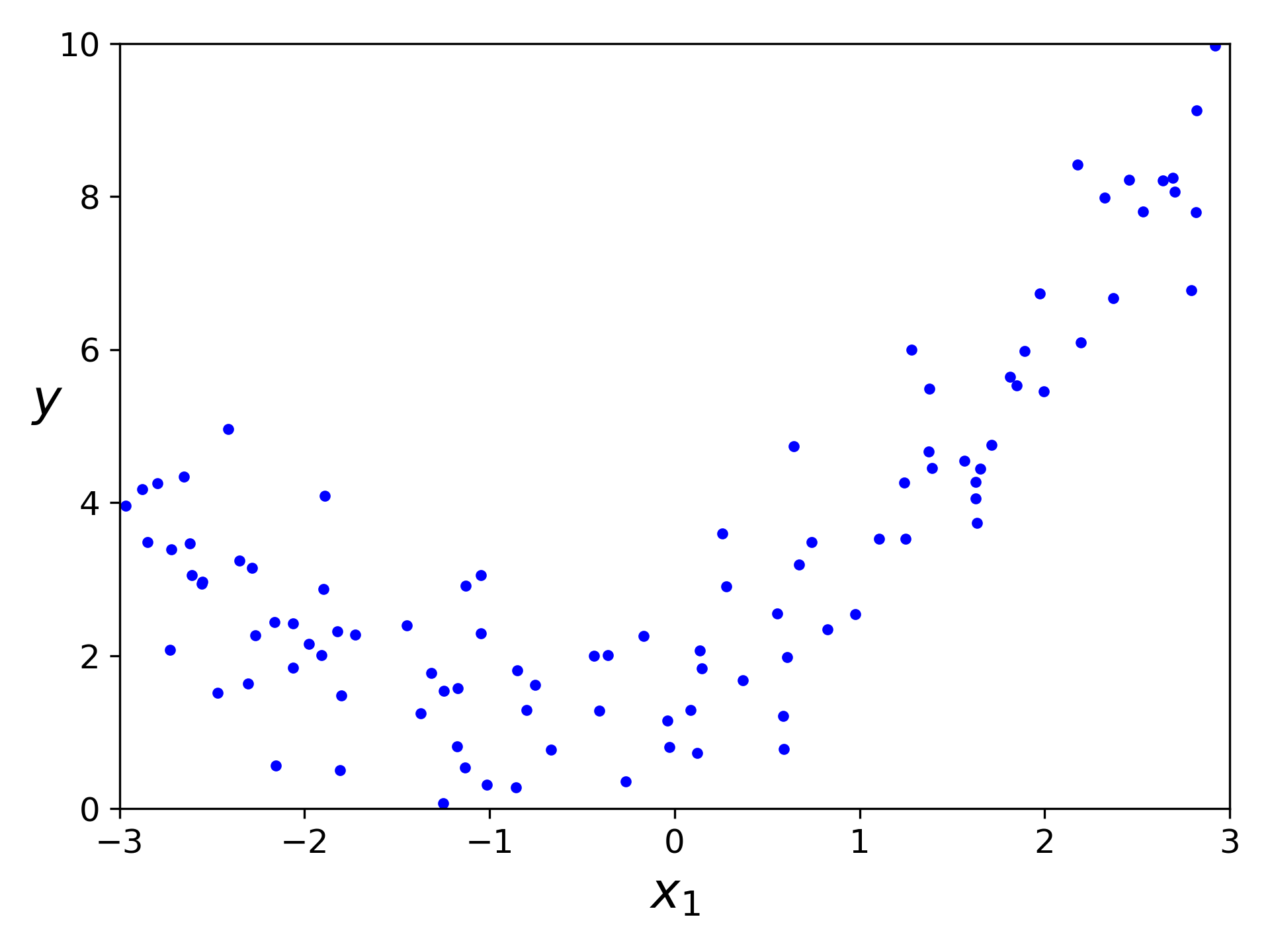
quadratic data plot

使用 PolynomialFeatures 类转换训练数据

将训练集中每个特征的评分（二次多项式）添加为新特征；

>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2, include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([-0.75275929])

>>> X_poly[0]   # 包含 X 的原始特征以及该特征的平方
array([-0.75275929,  0.56664654])

将 LinearRegression 模型拟合到该扩展训练数据中；

>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X_poly, y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([1.78134581]), array([[0.93366893, 0.56456263]]))

即模型估算：y^=0.56x12+0.93x1+1.78\hat{y} = 0.56x_1^2 + 0.93x_1 + 1.78（与原始函数相符：y=0.5x12+1.0x1+2.0+GaussianNoisey=0.5x_1^2 + 1.0x_1 + 2.0 + Gaussian Noise ）

多项式回归曲线

X_new = np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
plt.show()

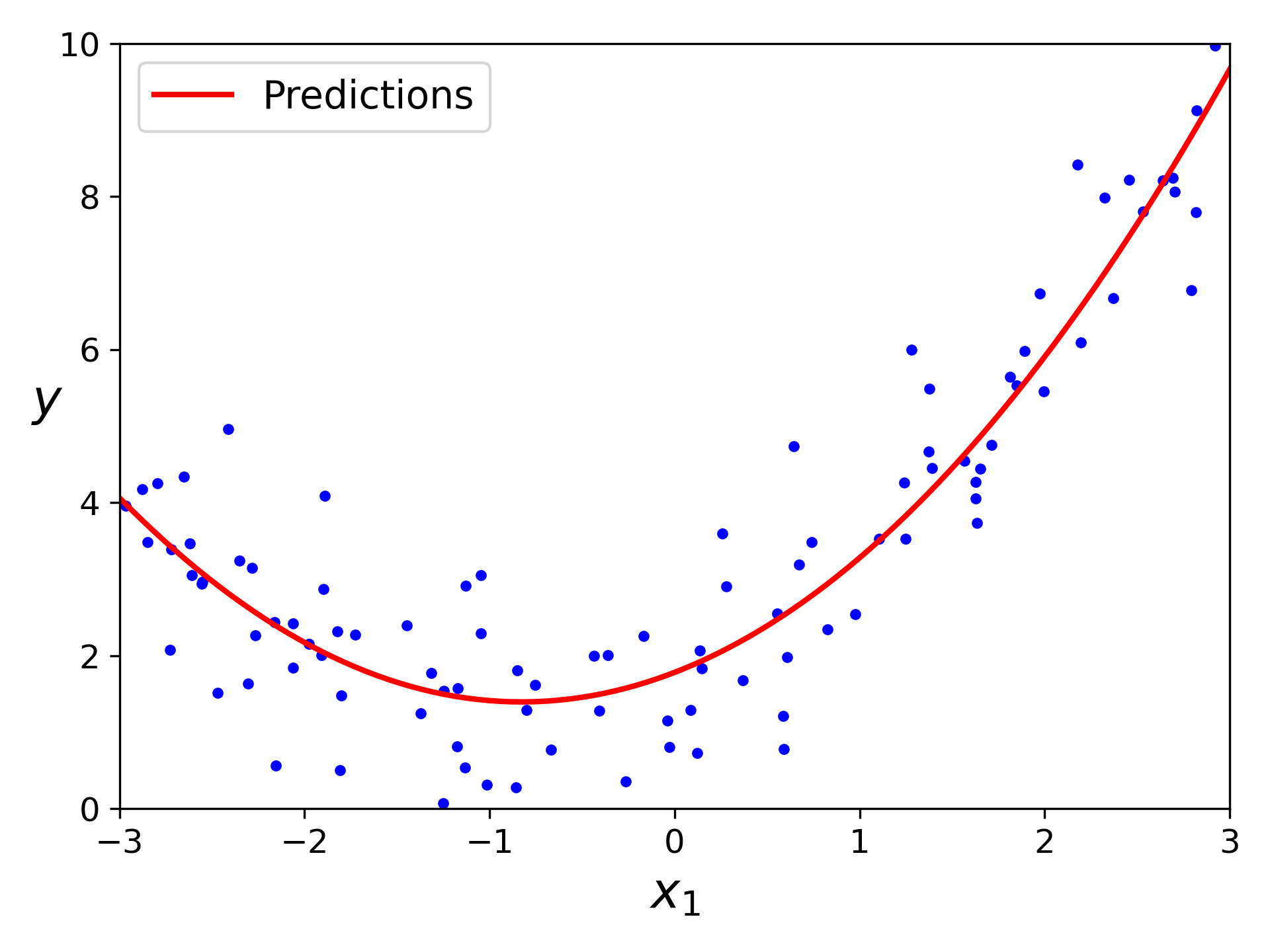
quadratic predictions plot

存在多个特征时，多项式回归能够找到特征之间的关系；PolynomialFeatures 可以将特征的所有组合添加到给定的多项式阶数（如存在两个特征 a 和 b，degress=3 的 PolynomialFeatures 不仅会添加特征 a2,a3,b2,b3a^2, a^3, b^2, b^3，还会添加组合 ab,a2b,ab2ab, a^2b, ab^2）；

PolynomialFeatures（degree=d）可以将一个包含 n 个特征的数组转换为包含 (n+d)!d!n!\frac{(n+d)!}{d!n!} 个特征的数组；因此要小心特征组合的数量爆炸；

4. 学习曲线​

高阶多项式回归的拟合曲线

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
    polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
    std_scaler = StandardScaler()
    lin_reg = LinearRegression()
    polynomial_regression = Pipeline([
        ("poly_features", polybig_features),
        ("std_scaler", std_scaler),
        ("lin_reg", lin_reg),
    ])
    polynomial_regression.fit(X, y)
    y_newbig = polynomial_regression.predict(X_new)
    plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)

plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
plt.show()

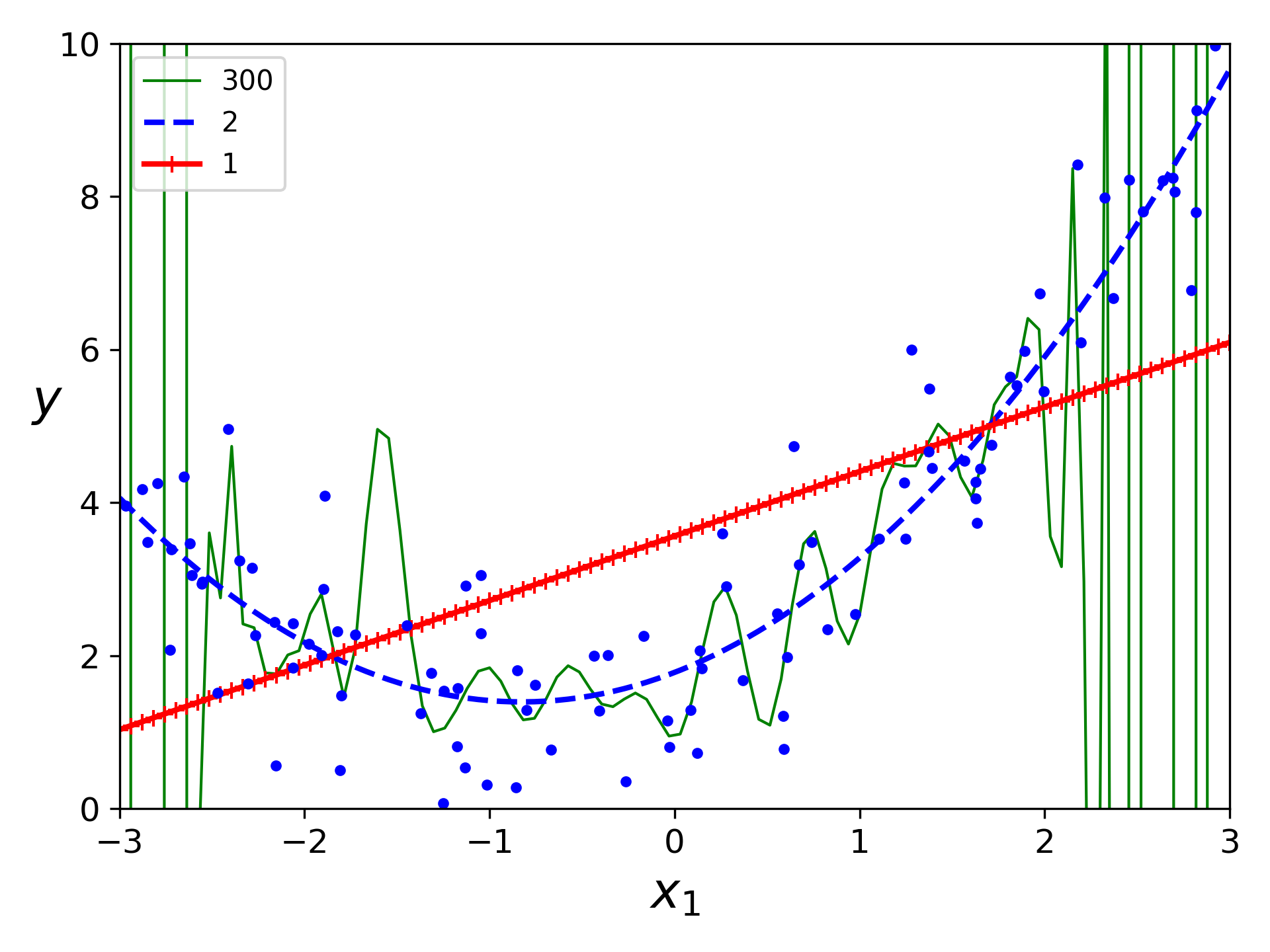
high degree polynomials plot

高阶多项式回归模型严重过拟合训练数据，而线性模型欠拟合，二次模型最能泛化数据集（数据就是使用二次模型生成的）；

评估模型泛化性能的方法

  • 交叉验证
    • 若模型在训练数据上表现良好，但交叉验证的指标泛化性能较差，则模型过拟合；
    • 若模型在训练数据和交叉验证表现都较差，则说明欠拟合；
  • 学习曲线：绘制模型在训练集和验证集上关于训练集大小（或训练迭代）的性能函数；在不同大小的训练子集上多次训练模型，观察期分别在训练集和验证集上的性能表现；

学习曲线函数

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split


def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(
        X, y, test_size=0.2, random_state=10)
    train_errors, val_errors = [], []
    for m in range(1, len(X_train) + 1):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))

    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
    plt.legend(loc="upper right", fontsize=14)
    plt.xlabel("Training set size", fontsize=14)
    plt.ylabel("RMSE", fontsize=14)

分别截取前 1、2、... m 个实例作为训练集进行训练，绘制其训练集和测试集上的性能效果；

普通线性回归模型的学习曲线

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.axis([0, 80, 0, 3])
plt.show()

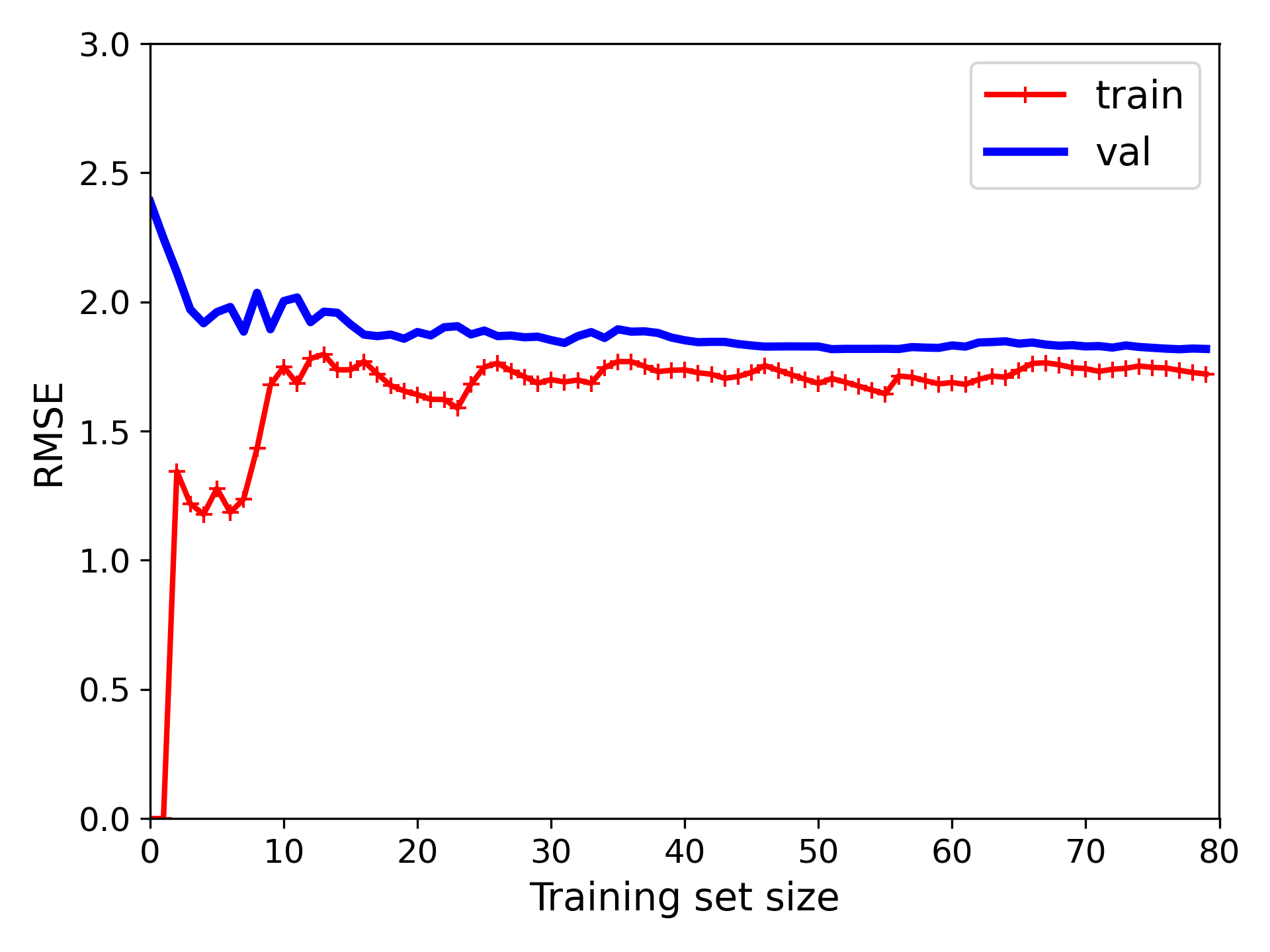
underfitting learning curves plot

当训练集只有一个或两个实例时，模型可以很好的拟合训练集（ train 曲线的 RMSE 从零开始），但无法正确泛化验证集（val 曲线误差很大）；随着新实例的加入，模型不能完美拟合训练数据（数据有噪声，且并非线性），但随着不断学习，验证集误差逐渐降低，训练集误差会一直上升，直到达到平稳状态；两条曲线最终接近，但误差停留在较高的位置；这说明模型是欠拟合训练集，且添加更多训练实例也无济于事，可能需要更复杂的模型或提供更好的特征；

10 阶多项式模型的学习曲线

from sklearn.pipeline import Pipeline

polynomial_regression = Pipeline([
    ("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
    ("lin_reg", LinearRegression()),
])

plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3])
plt.show()

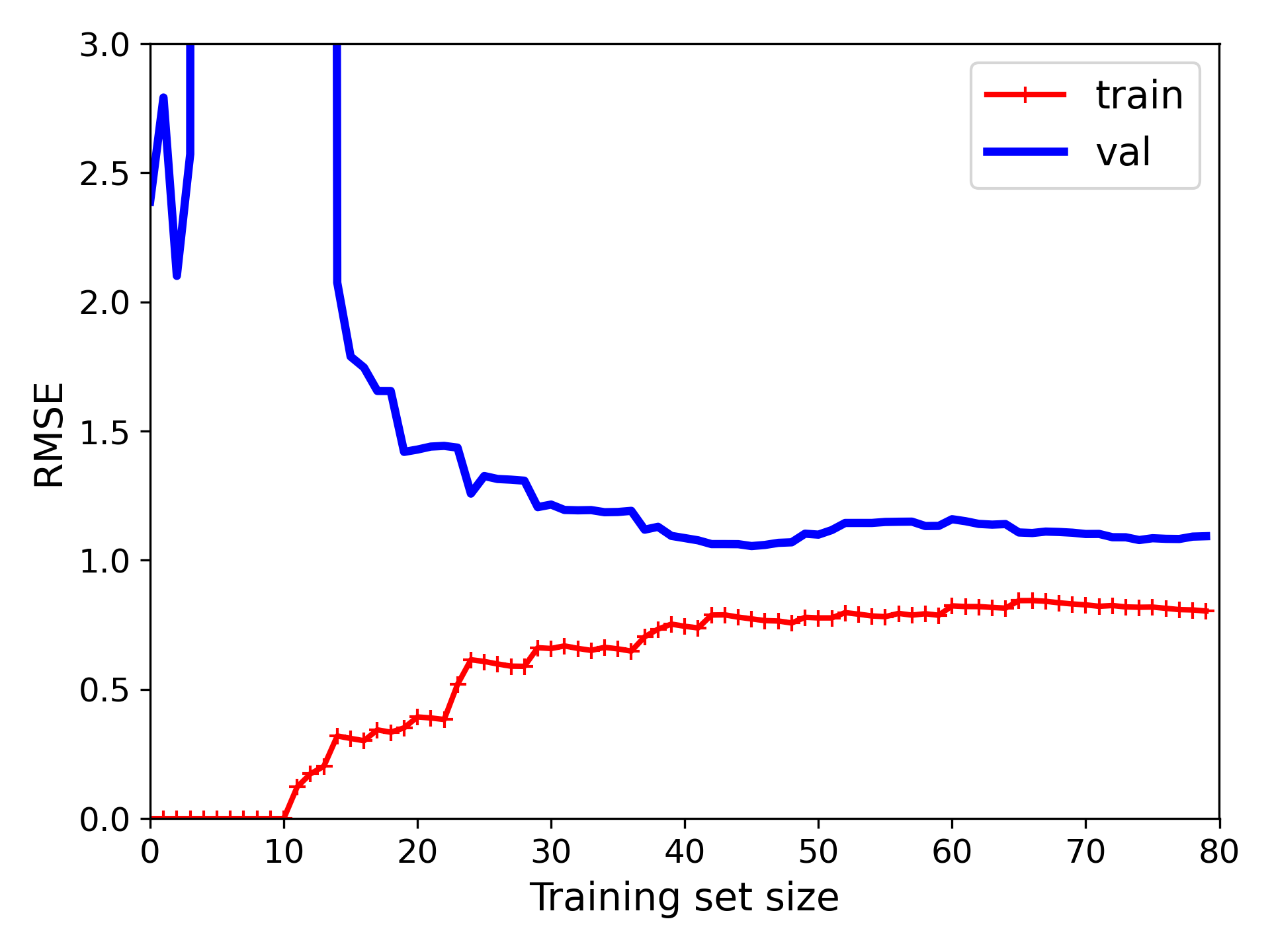
learning curves plot

  • 与普通线性回归模型相比，训练数据上的误差低了很多（2 -> 1）；
  • train 与 val 曲线之间的间隙更大，说明该模型在训练集上的性能要比在验证集上的性能要好很多，这说明模型过拟合，不过若使用更大的训练集，两条曲线会继续接近；

偏差与方差的权衡

统计学和机器学习的事实：模型的泛化误差可以表示为偏差、方差、不可避免的误差这三个非常不同的误差之和；

  • 偏差，错误的假设，如假设数据是线性的，而实际是二次的；高偏差模型可能欠拟合训练数据；
  • 方差，模型对训练数据的细微变化过于敏感，自由度越高可能方差越大，如高阶多项式模型，因此可能过拟合训练数据；
  • 不可避免的误差，数据本身的噪声，减少该误差的办法唯有清理数据（如修复数据源、检查并移除异常值等）；

增加模型复杂度通查会显著提升模型的方差并减少偏差，反之降低模型复杂度则会提升模型的偏差并降低方差，这其中需要试具体应用场景来权衡；

5. 正则化线性模型​

  • 正则化，即约束模型，线性模型通常通过约束模型的权重来实现；一种简单的方法是减少多项式的次数；模型拥有的自由度越小，则过拟合数据的难度就越大；

1. 岭回归​

  • 岭回归，也称 Tikhonov 正则化，线性回归的正则化版本，将等于 α∑i=1nθi2\alpha \sum_{i=1}^{n}\theta_i^2 的正则化项添加到成本函数；迫使学习算法拟合数据，使模型权重尽可能小；

仅在训练期间将正则化项添加到成本函数中，训练完模型后，使用非正则化的性能度量来评估模型的性能；好的训练成本函数应该具有对优化友好的导数，而用于测试的性能指标应该尽可能的接近最终目标（如使用成本函数如对数损失来训练分类器，但使用精度/召回率对其进行评估）；

岭回归的成本函数

J(θ)=MSE(θ)+α12∑i=1nθi2 J(\theta) = MSE(\theta) + \alpha \frac{1}{2} \sum_{i=1}^{n} \theta_i^2
  • α\alpha，控制要对模型进行正则化的程度的超参数，若 α\alpha = 0，则岭回归仅是一个线性回归，若 α\alpha 非常大，则所有权重最终都非常接近于零，结果是一条经过数据均值的平线；
  • θi\theta_i 从 θ1\theta_1 开始，偏置项 θ0\theta_0 没有进行正则化；

若定义 w 为特征权重的向量（θ1\theta_1 至 θn\theta_n），则正则项等于 12(∥w∥2)2\frac{1}{2}(\lVert w\lVert_2)^2，其中 ∥w∥2\lVert w\lVert_2 表示权重向量的 ℓ2\ell_2 范数；

岭回归对输入特征的缩放敏感，因此知悉岭回归之前需要缩放数据（如使用 StandardScaler）；

不同 α\alpha 值对线性数据训练的几种岭回归模型

>>> np.random.seed(42)
>>> m = 20
>>> X = 3 * np.random.rand(m, 1)
>>> y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
>>> X_new = np.linspace(0, 3, 100).reshape(100, 1)

使用 AndreLouis Cholesky 矩阵分解技术，执行岭回归（闭式解）；

>>> from sklearn.linear_model import Ridge
>>> ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
>>> ridge_reg.fit(X, y)
>>> ridge_reg.predict([[1.5]])
array([[1.55071465]])
>>> ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
>>> ridge_reg.fit(X, y)
>>> ridge_reg.predict([[1.5]])
array([[1.55072189]])
from sklearn.linear_model import Ridge


def plot_model(model_class, polynomial, alphas, **model_kargs):
    for alpha, style in zip(alphas, ("b-", "g--", "r:")):
        model = model_class(
            alpha, **model_kargs) if alpha > 0 else LinearRegression()
        if polynomial:
            model = Pipeline([
                ("poly_features", PolynomialFeatures(
                    degree=10, include_bias=False)),
                ("std_scaler", StandardScaler()),
                ("regul_reg", model),
            ])
        model.fit(X, y)
        y_new_regul = model.predict(X_new)
        lw = 2 if alpha > 0 else 1
        plt.plot(X_new, y_new_regul, style, linewidth=lw,
                 label=r"$\alpha = {}$".format(alpha))
    plt.plot(X, y, "b.", linewidth=3)
    plt.legend(loc="upper left", fontsize=15)
    plt.xlabel("$x_1$", fontsize=18)
    plt.axis([0, 3, 0, 4])


plt.figure(figsize=(8, 4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
plt.show()
  • 左：普通岭模型，线性预测；
  • 右：带有岭正则化的多项式回归；使用 PolynomialFeatures(degree=10) 扩展数据，使用 StandardScaler 进行缩放，最后将岭模型应用于结果特征；

随着 α\alpha 的增加，预测更平坦（不极端、更合理），模型的方差减少，偏差增加；

ridge regression plot

闭式解的岭回归

θ^=(XTX=αA)−1XTy \hat{\theta} = (X^T X=\alpha A)^{-1}X^T y
  • A 是 (n+1)×(n+1)(n+1) \times (n+1) 单位矩阵；

使用随机梯度下降

>>> sgd_reg = SGDRegressor(penalty="l2")
>>> sgd_reg.fit(X, y.ravel())
>>> sgd_reg.predict([[1.5]])
array([1.47012588])

超参数 penalty 设置的是使用正则项的类型，12 表示希望 SGD 在成本函数中添加一个正则项，等于权重向量的 ℓ2\ell_2 范数的平方的一半，即岭回归；

2. Lasso 回归​

  • Lasso 回归，最小绝对收缩和选择算子回归（Least Absolute Shrinkage and Selection Operator Regression，简称 Lasso 回归），向成本函数添加一个正则项（权重向量的 ℓ1\ell_1 范数）；

Lasso 回归成本函数

J(θ)=MSE(θ)+α∑i=1n∣θi∣ J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} \lvert \theta_i \lvert

使用不同级别的 Lasso 正则化

from sklearn.linear_model import Lasso

plt.figure(figsize=(8, 4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)

plt.show()

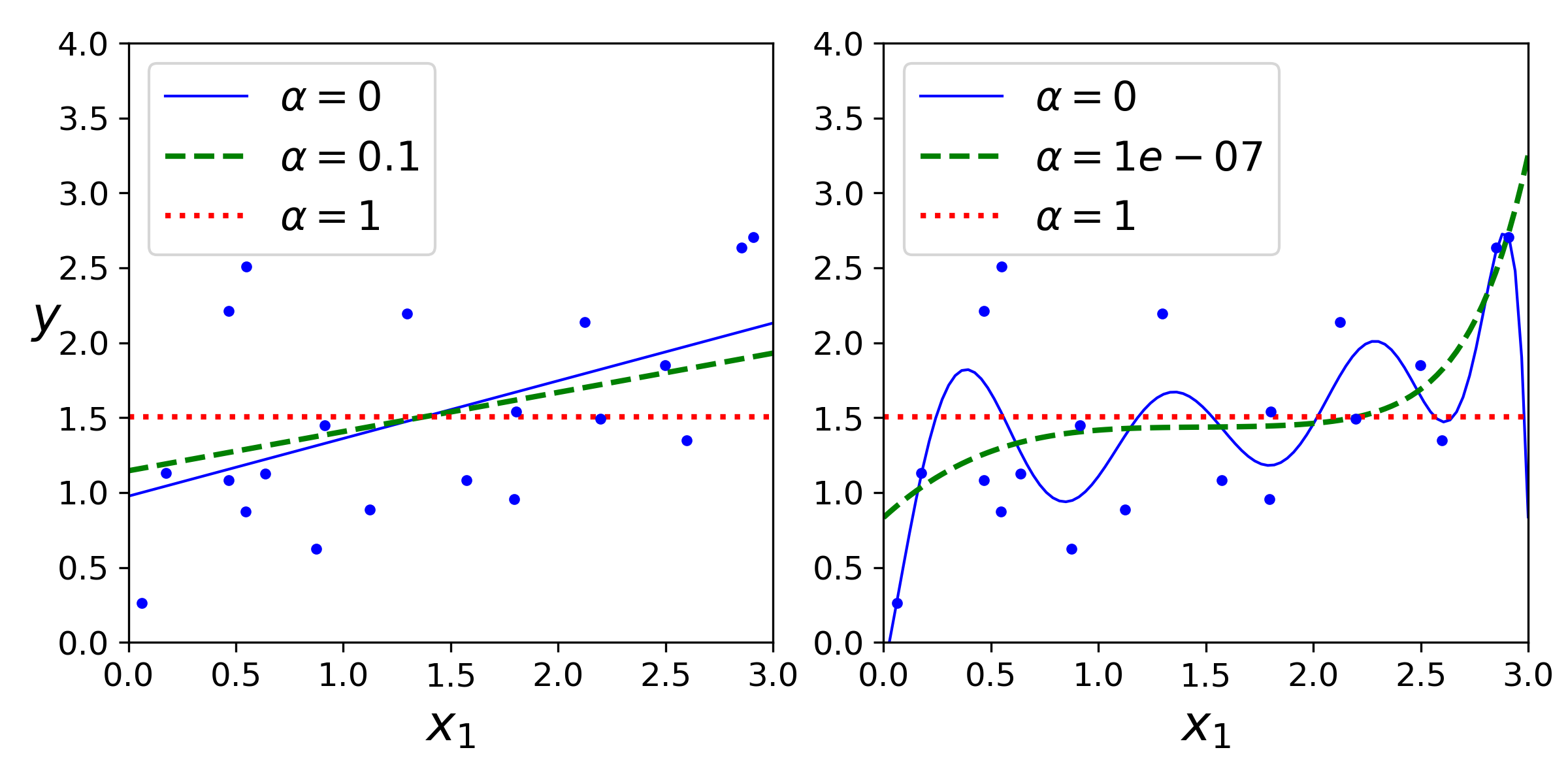
lasso regression plot

Lasso 回归倾向于完全消除掉最不重要的特征的权重；（α=10−7\alpha = 10^{-7} 看起来像二次的，因为所有高阶多项式的特征权重都等于零）；Lasso 回归会自动执行特征选择并输出一个稀疏模型（只有很少的特征有非零权重）；

Lasso 成本函数在 θ=0\theta = 0 处是不可微的，可以使用子梯度向量 g 代替任何 θi=0\theta_i = 0;

带有 Lasso 成本函数的梯度下降的子梯度向量方程

g(θ,J)=∇θMSE(θ)+α(sin(θ1)sin(θ2)...sin(θn)),sin(θi)={−1  ifθi<00  ifθi=0+1  ifθi>0 g(\theta, J) = \nabla_{\theta} MSE(\theta) + \alpha \begin{pmatrix} sin(\theta_1) \\ sin(\theta_2) \\ ... \\ sin(\theta_n) \end{pmatrix}, sin(\theta_i) = \begin{cases} -1 \; if \theta_i < 0 \\ 0 \; if \theta_i = 0 \\ +1 \; if \theta_i > 0 \end{cases}

3. 弹性网络​

  • 弹性网络，介于岭回归和 Lasso 回归之间的中间地带，正则项式岭和 Lasso 正则项的简单混合，通过 r 控制混合比；r=0 时，弹性网络等效于岭回归，r=1 时，弹性网络等效于 Lasso 回归；

弹性网络成本函数

J(θ)=MSE(θ)+rα∑i=1n∣θi∣+1−r2α∑i=1nθi2 J(\theta) = MSE(\theta) + r\alpha \sum_{i=1}^{n} \lvert \theta_i \lvert + \frac{1-r}{2} \alpha \sum_{i=1}^{n} \theta_i^2
  • 通常有正则化比没有更可取，大多数情况下应避免纯线性回归；此时岭回归是不错的默认选择；
  • 当实际用到的特征只有少数几个，可以考虑 Lasso 回归或弹性网络，它们会将无用特征的权重降为零；
  • 弹性网络一半由于 Lasso 回归，特征数据超过实例数量，或者几个特征强相关时，Lasso 回归表现可能很不稳定；

ElasticNet 示例

>>> from sklearn.linear_model import ElasticNet
>>> elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
>>> elastic_net.fit(X, y)
>>> elastic_net.predict([[1.5]])
array([1.54333232])

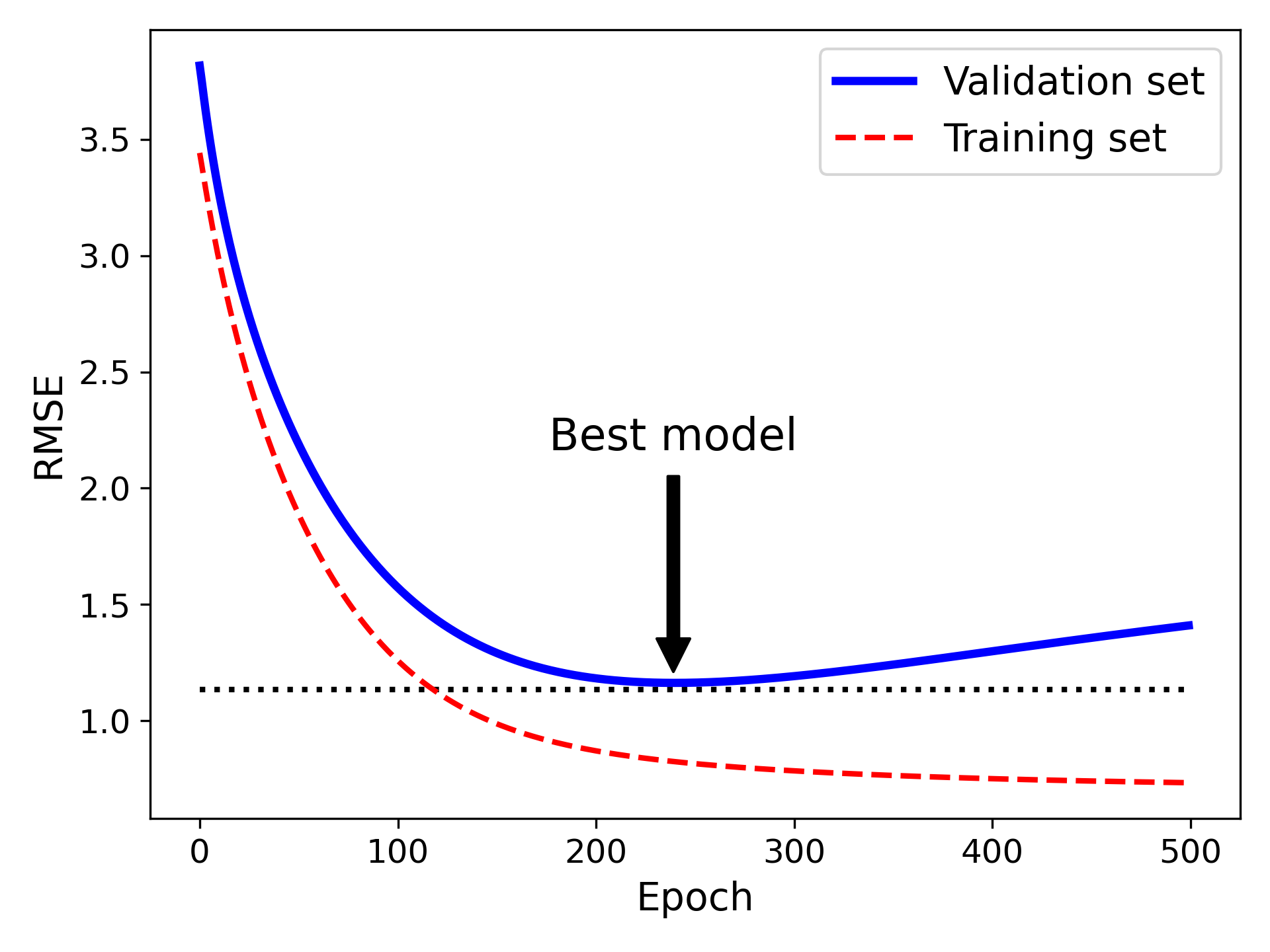
4. 提前停止​

  • 提前停止，对于梯度下降这类迭代学习算法，在验证误差达到最小值时停止训练；通过早期停止法，一旦验证误差达到最小值就立刻停止训练；

early stopping plot

随机和小批量梯度下降时，曲线不是平滑的，可能很难知道是否达到最小值，此时可以仅在验证错误超过最小值一段时间后停止（确信模型不会做到更好时），然后回滚模型参数到验证误差最小的位置；

提前停止法示例

np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)

X_train, X_val, y_train, y_val = train_test_split(
    X[:50], y[:50].ravel(), test_size=0.5, random_state=10)
from copy import deepcopy

poly_scaler = Pipeline([
    ("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
    ("std_scaler", StandardScaler())
])

X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)

sgd_reg = SGDRegressor(max_iter=1, warm_start=True, penalty=None,
                       learning_rate="constant", eta0=0.0005, random_state=42)

minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
    sgd_reg.fit(X_train_poly_scaled, y_train)  # continues where it left off
    y_val_predict = sgd_reg.predict(X_val_poly_scaled)
    val_error = mean_squared_error(y_val, y_val_predict)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = deepcopy(sgd_reg)

warm_start=True 表示调用 fit() 方法时，在停止的地方继续训练，而不是从头开始；

6. 逻辑回归​

  • 逻辑回归，Logistic 回归，Logit 回归，广泛应用于估算一个示例属于某个特定类别的概率；（二元分类器：预估概率高于 50% 则模型预测该实例属于该类别，称正类，反之则预测不是该类别，称负类）；

1. 估计概率​

逻辑回归模型也是计算输入特征的加权和（加上偏置项），但不同于线性回归模型直接输出结果，它输出的是梳理逻辑值；

逻辑回归模型的估计概率（向量化形式）

p^=hθ(x)=σ(xTθ) \hat{p} = h_\theta(x) = \sigma(x^T\theta)

逻辑函数

σ(t)=11+exp(−t) \sigma(t) = \frac{1}{1+exp(-t)}

分数 t 称为 logit，估计概率 p 的对上；logit(p) = log(p/(1-p))，与 logistic 函数相反； 对数也称对数奇数，是正类的估计概率与父类的估计概率之比的对数；

t = np.linspace(-10, 10, 100)
sig = 1 / (1 + np.exp(-t))
plt.figure(figsize=(9, 3))
plt.plot([-10, 10], [0, 0], "k-")
plt.plot([-10, 10], [0.5, 0.5], "k:")
plt.plot([-10, 10], [1, 1], "k:")
plt.plot([0, 0], [-1.1, 1.1], "k-")
plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$")
plt.xlabel("t")
plt.legend(loc="upper left", fontsize=20)
plt.axis([-10, 10, -0.1, 1.1])
plt.show()

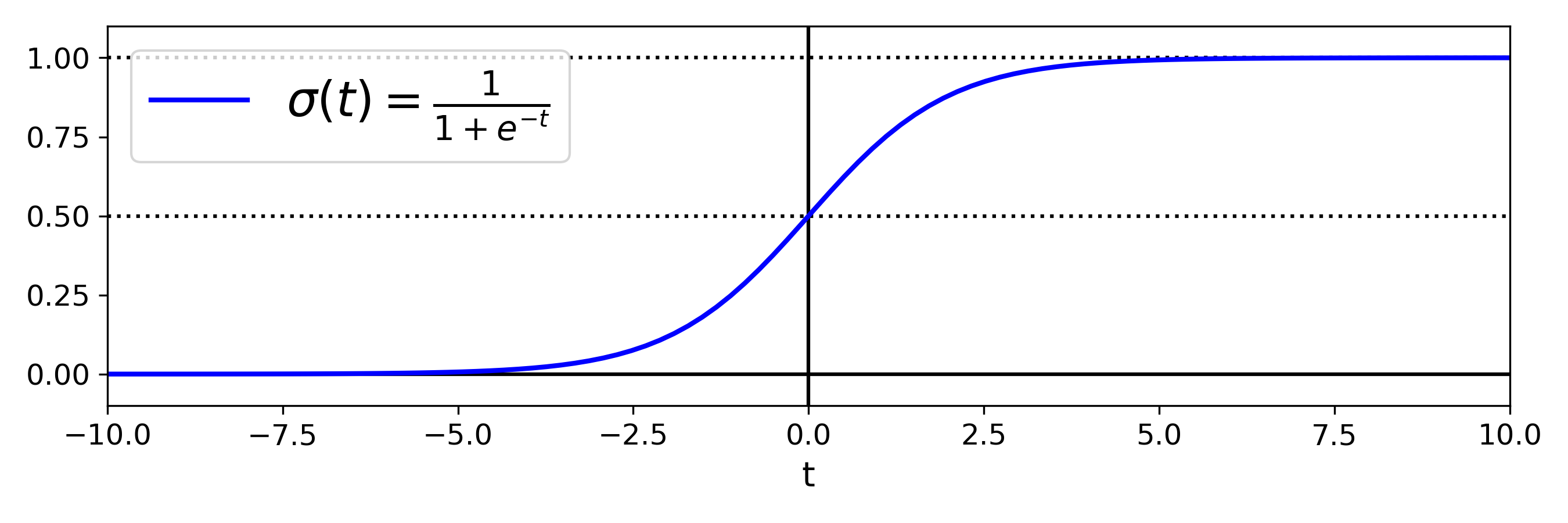
logistic function plot

逻辑回归模型估算出实例 x 属于整理的概率 p^=hθ(x)\hat{p} = h_\theta(x)，就可以预测 y^\hat{y}

逻辑回归模型预测

y^={0,ifp^<0.51,ifp^≥0.5 \hat{y} = \begin{cases} 0, if \hat{p} < 0.5 \\ 1, if \hat{p} \geq 0.5 \end{cases}

当 t<0t < 0 时，σ(t)<0.5\sigma(t) < 0.5；当 t≥0t \geq 0 时，σ(t)≥0.5\sigma(t) \geq 0.5；因此若 XTθX^T\theta 是正类，逻辑回归模型预测结果就是 1，若是负类，则预测结果为 0；

2. 训练和成本函数​

训练的目的是设置参数向量 θ\theta，是模型对正类实例做出高概率估算，对负类实例做出低概率估算；

单个训练实例的成本函数

c(θ)={−log(p^),ify=1−log(1−p^),ify=0 c(\theta) = \begin{cases} -log(\hat{p}), if y=1 \\ -log(1-\hat{p}), if y=0 \end{cases}

当 t 接近 0 时，-log(t) 会变得非常大，若模型估算一个正类实例的概率接近与 0，成本降变得很高；负类实例同理；对一个负类实例估算概率接近 0，对一个正类实例估算概率接近与 1，而成本则都解决与 0，这正式我们想要的；

逻辑回归成本函数（对数损失）

整个训练集的成本函数是所有训练实例的平均成本，可以用一个对数损失单一表达式表示；

J(θ)=−1m∑i=1m[yilog(p^i)+(1−y(i))log(1−p^(i))] J(\theta) = -\frac{1}{m} \sum_{i=1}^{m}[y^{i} log(\hat{p}^i) + (1-y^{(i)})log(1 - \hat{p}^{(i)})]

该函数没有已知的闭式方程（不存在一个标准方程的等价方程）来计算出最小化成本函数的 θ\theta 值；但这是一个凸函数，通过梯度下降等任意优化算法可以找出全局最小值（学习率不太高、运行足够长时间的情况下）；

逻辑成本函数偏导数

∂∂θjJ(θ)=1m∑i=1m(σ(θTx(i))−y(i))xj(i) \frac{\partial}{\partial\theta_j} J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (\sigma (\theta^Tx^{(i)}) - y^{(i)}) x_j^{(i)}

对每个实例计算预测误差并将其乘以第 j 个特征值，然后计算所有训练实例的平均值；有了包含所有偏导数的梯度向量，就可以使用梯度下降算法；

3. 决策边界​

基于花瓣宽度特征，创建一个分类器检测维吉尼亚鸢尾花

>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> list(iris.keys())
['data',
 'target',
 'frame',
 'target_names',
 'DESCR',
 'feature_names',
 'filename',
 'data_module']

>>> print(iris.DESCR)
.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica

    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
...
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...
>>> X = iris["data"][:, 3:]  # petal width
>>> y = (iris["target"] == 2).astype(np.int64)  # 1 if Iris virginica, else 0

训练一个逻辑回归模型

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)

花瓣宽度在 0 到 3cm 之间的鸢尾花，模型估算出的概率如下；

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0][0]

plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision  boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
plt.show()

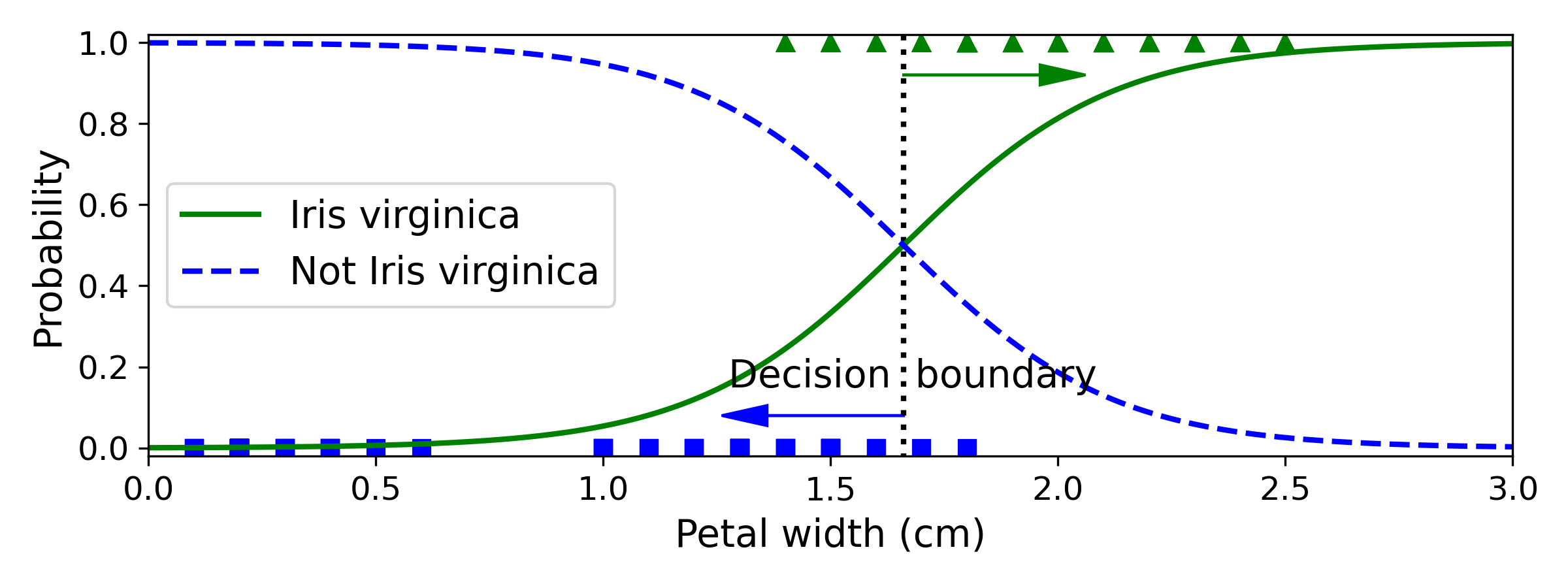
logistic regression plot

维吉尼亚鸢尾花（三角形）的花瓣宽度范围为 1.4 ~ 2.5 cm，其他两种鸢尾花（正方形）花瓣宽度范围为 0.1 ~ 1.8 cm，存在一部分重叠；

花瓣宽度超过 2cm 的花和低于 1cm 的花可以很明确其分别对应维吉尼亚鸢尾花和非维吉尼亚鸢尾花（对正类和负类输出了高概率值），而两个极端中间部分不太好把握，只能返回一个可能性最大的类别，概率相等处表示正类和父类的可能性都是 50%，这就是一个决策边界；

基于花瓣宽度和花瓣长度两个特征，创建一个分类器检测维吉尼亚鸢尾花

from sklearn.linear_model import LogisticRegression

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.int64)

log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)

x0, x1 = np.meshgrid(
    np.linspace(2.9, 7, 500).reshape(-1, 1),
    np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = log_reg.predict_proba(X_new)

plt.figure(figsize=(10, 4))
plt.plot(X[y == 0, 0], X[y == 0, 1], "bs")
plt.plot(X[y == 1, 0], X[y == 1, 1], "g^")

zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)


left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right +
             log_reg.intercept_[0]) / log_reg.coef_[0][1]

plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
plt.show()

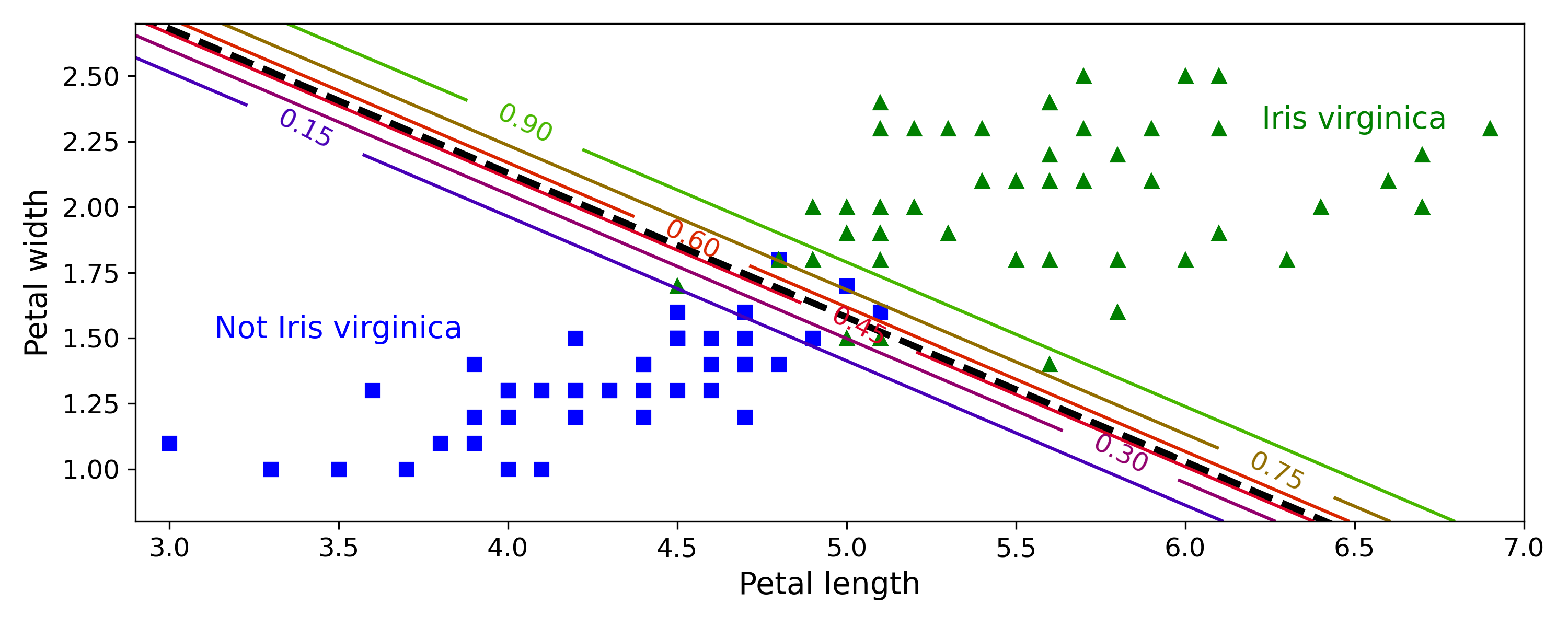
logistic regression contour plot

虚线表示模型估算概率为 50% 的点，即模型的决策边界（线性的边界，每条平行线代表一个模型输出的特定概率）；

  • 逻辑回归模型可以用 ℓ1\ell_1 或 ℓ2\ell_2 惩罚函数来正则化，Scikit-Learn 默认添加 ℓ2\ell_2 函数；
  • C，Scikit-Learn LogisticRegression 模型的正则化强度超参数，α\alpha 的反值，C 值越高，对模型的正则化越少；

4. Softmax 回归​

Softmax 回归，又叫多元逻辑回归，逻辑回归模型的推广，可以直接支持多个类别（每次只能预测一个类，即多类而非多输出，只能与互斥的类一起使用），而不需训练并组合多个二元分类器；

类 k 的 Softmax 分数

Sk(x)=xTθ(k) S_k(x) = x^T\theta^{(k)}

给定一个实例 x，Softmax 回归模型先计算出每个类 k 的分数 Sk(x)S_k(x)，然后对这些分数应用 softmax 函数（归一化指数）估算出每个类的概率；

每个类有自己的特定参数向量 θk\theta^{k}，所有这些向量通常作为行存储在参数矩阵 Θ\Theta；

Softmax 函数

p^k=σ(s(x))k=exp(sk(x))∑j=1Kexp(sj(x)) \hat{p}_k = \sigma(s(x))_k = \frac{exp(s_k(x))}{\sum_{j=1}^{K} exp(s_j(x))}
  • K，类数；
  • s(x)，一个向量，包含实例 x 的每个类的分数；
  • σ(s(x))k\sigma(s(x))_k，实例 x 属于类 k 的估计概率，给定该实例每个类的分数；

Softmax 回归分类预测

y^=argmaxk  σ(s(x))k=argmaxk  sk(x)=argmaxk((θ(k))Tx) \hat{y} = argmax_k \; \sigma(s(x))_k = argmax_k \; s_k(x) = argmax_k((\theta^{(k)})^Tx)

argmax 运算符返回使函数最大化的变量值；此处返回使估计概率 σ(s(x))k\sigma(s(x))_k 最大化的 k 值；

交叉熵成本函数

通常用于衡量一组估算出的类概率跟目标类的匹配程度；

J(Θ)=−1m∑i=1m∑k=1Kyk(i)log(p^k(i)) J(\Theta) = - \frac{1}{m} \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} log(\hat{p}_k^{(i)})
  • yk(i)y_k^{(i)}，属于类 k 的第 i 个实例的目标概率，一般为 1 或 0，表示实例是否属于该类；

当只有两个类（K=2）时，此成本函数等效于逻辑回归的成本函数（对数损失）；

类 k 的交叉熵梯度向量

成本函数相对于 θ(k)\theta^{(k)} 的梯度向量；计算每个类的梯度向量，然后使用梯度下降（或其他任意优化算法）找到最小化成本函数的参数矩阵 Θ\Theta；

∇θ(k)J(Θ)=1m∑i=1m(p^k(i)−yk(i))x(i) \nabla_{\theta(k)}J(\Theta) = \frac{1}{m} \sum_{i=1}^{m} (\hat{p}_k^{(i)} - y_k^{(i)}) x^{(i)}

使用 Softmax 回归将鸢尾花分为三类

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
  • LogisticRegressio 默认使用一对多的训练方式，设置超参数 multi_class 为 multinomial 可以切换为 Softmax 回归；
  • solver="lbfgs"，指定支持 Softmax 回归的求解器；
  • C，正则化超参数，默认使用 ℓ2\ell_2 正则化;
from matplotlib.colors import ListedColormap
x0, x1 = np.meshgrid(
    np.linspace(0, 8, 500).reshape(-1, 1),
    np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]


y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y == 2, 0], X[y == 2, 1], "g^", label="Iris virginica")
plt.plot(X[y == 1, 0], X[y == 1, 1], "bs", label="Iris versicolor")
plt.plot(X[y == 0, 0], X[y == 0, 1], "yo", label="Iris setosa")

custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()

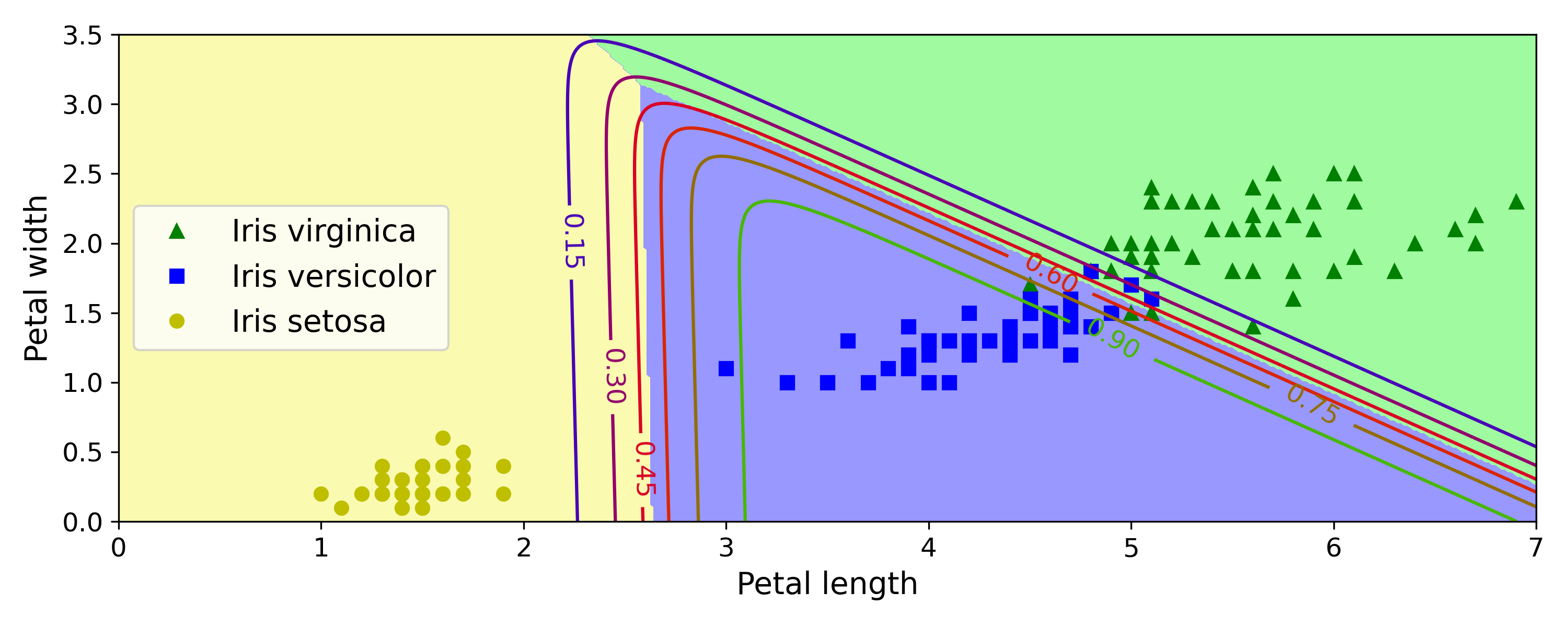
softmax regression contour plot

任何两个类之间的决策边界都是线性的，估算概率可能是低于 50% 的，在所有决策边界相交的地方，所有类的估算概率都为 33%；

>>> softmax_reg.predict([[5, 2]])
array([2])

>>> softmax_reg.predict_proba([[5, 2]])
array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

花瓣长 5cm，宽 2cm，模型预测结果为 94.2% 是维吉尼亚鸢尾，5.8% 是变色鸢尾；

欢迎各路道友阅读与评论，感谢道友点赞、关注、收藏！

参考资料：

  • [1]《机器学习》
  • [2]《机器学习实战》